решение на фотографиях
Пошаговое объяснение:
1) Линейное ДУ. Используем замену.
2) Однородное ДУ. Используем замену.
3) ДУ 2 порядка, допускающее понижение порядка. Используем замену.
4) Неоднородное линейное ДУ. Решено с метода неопределенных коэффициентов. Первым действием решаем ОЛДУ (однородное линейное ДУ). Вторым подбираем y~, дифференцируем, подставляем все это в НЛДУ, находим. В ответе к у из 1) прибавляем у~ из 2).
5) Все то же НЛДУ, но уже решаем методом вариации произвольных постоянных. Постаралась вкратце формулами расписать, надеюсь, понятно. Находим главный определитель (W), а в W1 и W2 на месте 1 и 2 столбцов подставляем значения независимых членов, без переменных (Z'1(x) и Z'2(x)), я их выделила черным цветом. И еще сначала искала Z2(x), так как ошиблась со столбцом. Нашли определитель - его значение и будет являться Z'(1 или 2)(х). Осталась интегрировать, чтобы найти функцию без '. Готово. Не забываем прибавить ту часть функции, которую нашли в 1), и записываем ответ.
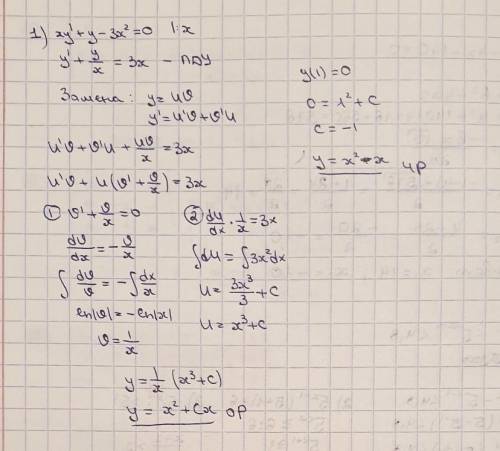



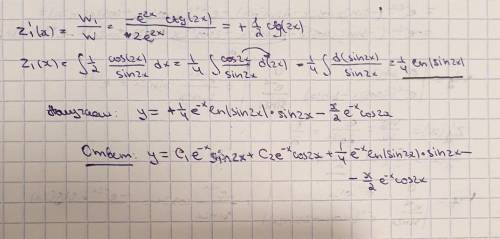
решай по формуле
Пошаговое объяснение:
V={\frac {1}{3}}Sh,
где S {\displaystyle \ S} \ S — площадь основания и h {\displaystyle \ h} \ h — высота;
V = 1 6 V p , {\displaystyle V={\frac {1}{6}}V_{p},} V={\frac {1}{6}}V_{p},
где V p {\displaystyle \ V_{p}} \ V_{p} — объём параллелепипеда;
Также объём треугольной пирамиды (тетраэдра) может быть вычислен по формуле[7]:
V = 1 6 a 1 a 2 d sin φ , {\displaystyle V={\frac {1}{6}}a_{1}a_{2}d\sin \varphi ,} V={\frac {1}{6}}a_{1}a_{2}d\sin \varphi ,
где a 1 , a 2 {\displaystyle a_{1},a_{2}} a_{1},a_{2} — скрещивающиеся рёбра , d {\displaystyle d} d — расстояние между a 1 {\displaystyle a_{1}} a_{1} и a 2 {\displaystyle a_{2}} a_{2} , φ {\displaystyle \varphi } \varphi — угол между a 1 {\displaystyle a_{1}} a_{1} и a 2 {\displaystyle a_{2}} a_{2};
Боковая поверхность — это сумма площадей боковых граней:
S b = ∑ i S i {\displaystyle S_{b}=\sum _{i}^{}S_{i}} S_{b}=\sum _{i}^{}S_{i}
Полная поверхность — это сумма площади боковой поверхности и площади основания:
S p = S b + S o {\displaystyle \ S_{p}=S_{b}+S_{o}} \ S_{p}=S_{b}+S_{o}
Для нахождения площади боковой поверхности в правильной пирамиде можно использовать формулы:
S b = 1 2 P a = n 2 b 2 sin α {\displaystyle S_{b}={\frac {1}{2}}Pa={\frac {n}{2}}b^{2}\sin \alpha } {\displaystyle S_{b}={\frac {1}{2}}Pa={\frac {n}{2}}b^{2}\sin \alpha }
где a {\displaystyle a} a — апофема , P {\displaystyle \ P} \ P — периметр основания, n {\displaystyle \ n} \ n — число сторон основания, b {\displaystyle \ b} \ b — боковое ребро, α {\displaystyle \alpha } \alpha — плоский угол при вершине пирамиды.