В общем случае, не всегда.
Действительно,
при делении на 7 в остатке
может быть 0, 1, 2, 3...6
Возьмём, например, 100 целых чисел, каждое из которых даёт остаток 1 при делении на 7.
то есть числа вида 7k+1, k€Z
Из них невозможно выбрать два числа, сумма которых кратна 7.
Действительно, пусть эти числа
(7k1+1 ) и (7k2+1)
(k1€Z, k2€Z)
сложим эти два числа :
(7k1+1)+(7k2+1) = 7(k1+ k2)+2
как мы видим, полученная сумма при делении на 7 даёт остаток 2, то есть не делится нацело на 7
ответ: нет, утверждение неверно
Теплоход весь путь от А до Б (по течению) и обратно (против течения) шел с максимальной скорость. Но действительно, в связи с наличием течения, скорость его была разной: от А до Б - 30 км/ч, а от Б до А - 20 км/час. Какова его средняя скорость движения на всем пути?
Средняя скорость движения парохода на всем пути Vcр определяется по формуле
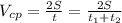
где 2S -весь путь пройденный пароходом (S-расстояние от А до Б)
t - полное время всего пути равное сумме времени по течению t₁ и против течения t₂.
Время по течению t₁ равно
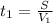
где V₁ = 30 км/ч -скорость парохода по течению
Время против течения t₂ равно
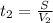
где V₂ = 20 км/ч -скорость парохода против течения
Поэтому полное время в пути равно
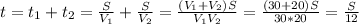
Средняя скорость парохода равна
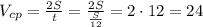 км/ч
км/ч
ответ 24 км/ч
длина - 3х
периметр = 2*(длина+ширина)
2*(3х+х)=64
2*4х=64
8х=64
х=64/8
х=8 см - это ширина
8*3=24 см - это длина