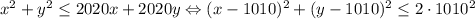, то есть это круг (с границей), с центром в точке 
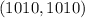и радиусом 
. Среди точек этого множества требуется найти такие, для которых 
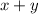принимает наибольшее значение. Понятно также, что никакая точка внутренности не является искомой, поскольку ее можно сдвинуть на вектор 
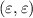для некоторого 
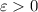. Потому точки ищем на границе.
Рассмотрим прямую 
. Требуется максимизировать 
, то есть увеличивать это значение до тех пор, пока эта прямая имеет пересечения с окружностью. Предельный случай -- касание. Имеем: 
, 
, откуда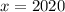 
. Тогда 
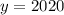и 
.
Для начала найдём область определения функции.
1)
Определим, является эта функция чётной, нечётной или же ни чётной, ни нечётной.
2) - следовательно, функция не является ни чётной, ни нечётной.
Найдём точки пересечения с осью Ox (y = 0).
3)
Найдём точки пересечения с осью Oy (x = 0).
4) Так как x ≠ 0 (см. область определения), то точек пересечения графика функции с осью Oy нет.
Найдём промежутки знакопостоянства.
5)
+ - +
оо> x
Функция положительна при .
Функция отрицательна при .
Найдём асимптоты графика функции.
6) вертикальная асимптота: .
Предел равен . Горизонтальных асимптот не существует, наклонных асимптот не существует.
Вычислим производную и найдём критические точки функции.
7)
Найдём промежутки монотонности функции, точки экстремума и значение функции в этих точках.
8)
- - + f'(x)
о> x
f(x)
Функция убывает при .
Функция возрастает при .
- точка минимума функции.
.
Вычислим вторую производную.
9)
Определим выпуклость функции и найдём точки перегиба.
10)
+ - +
оо> x
Функция выпукла вниз при .
Функция выпукла вверх при .
Точка перегиба: .
Определим множество значений функции.
11) .
