Пошаговое объяснение:
1) в рукопожатием принимают участие 2 человека, поэтому рукопожатие удваивается, т.е. умножается на 2
2)Под графом мы будем понимать множество точек (вершин), некоторые из которых соединены отрезками (ребрами).
Степень вершины графа — это количество выходящих из нее (или, что то же самое, входящих в нее) ребер (еще говорят: количество ребер, инцидентных данной вершине). Вершина графа называется четной, если ее степень четна, и нечетной в противном случае.
Некоторая часть вершин данного графа называется компонентой связности, если из любой ее вершины можно «дойти» до любой другой, двигаясь по ребрам.
В некоторых случаях на ребрах графа выбирается «направление движения» (например, когда на автомобильной дороге вводится одностороннее движение). При этом получается ориентированный граф. (Если направление движения по ребрам не определено, то граф называется неориентированным). В ориентированном графе различают положительную и отрицательную степень каждой вершины (то есть количество ребер, соответственно, входящих и выходящих из нее). Две вершины могут быть соединены и несколькими ребрами, направления движения по которым противоположны («дорога с двусторонним движением»). Изменяется понятие компоненты связности: теперь каждый «маршрут» от одной вершины до другой должен учитывать направление движения по ребрам.Теорема 2. Всякий (неориентированный) граф содержит четное число нечетных вершин. ответ. Нет.
Решение. Сделаем вассалов вершинами графа; ребрами соединим тех из них, которые являются соседями. По условию все вершины этого графа нечетны, а всего их 19, то есть тоже нечетное число. Но по теореме 2 такого быть не может.
Ну и задачка)
Число A имеет вид
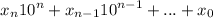
Число B (число А после перестановки) имеет вид
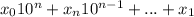
2А=B
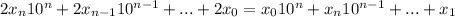
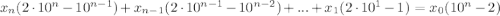
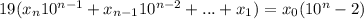
Далее анализируем. Выражение справа должно делиться на 19. Но так как 19 - простое число, а все коэффициенты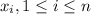 
являются цифрами, то есть натуральными числами с 1 по 9, то x0 не разделится на 19 никак, а значит, 
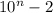делится на 19.
Признак делимости на 19 есть, конечно: число без последней цифры + удвоенная последняя цифра ( их сумма имеется в виду) должна делиться на 19. Можно применять последовательно. Но я как-то не вижу возможности в общем виде это расписать.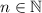 
, естественно. В общем, мучаясь и страдая, подбором получаем
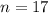
И поделив на 19 число 99999999999999998, получаем 5263157894736842. Но что это? Если посмотрим на выражение
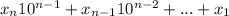
то станет ясно, что это записанное число до перестановки без последней цифры
а выражение справа получается
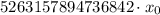
Теперь надо подобрать натуральное решение этого уравнения.
Анализируем возможные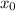 
1 быть не может, так как получится это же число, к нему в конец должна добавиться 1 (х0) но там спереди 5, а на будет конце 1, а при переставлении число должно удвоиться, а так как разрядность чисел одинакова, то старший коэффициент должен тоже минимум удвоиться, а здесь такого нет.
А вот что будет при 2:
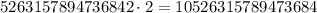
Удивительно, но при добавлении 2 в конце, которая потом пойдет вперед число вполне себе удваивается. Проверим
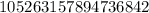
Переставив 2 в начало, получим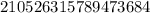 
Ну и поделив второе на первое, получим
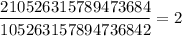
Работает. Удивительно, что Вере это число показалось малым))
ответ: 
Во втором 3/1000км больше 30дм
В третем 10/12 больше 42 с
В четвёртом 100/250 кг больше 100г
В пятом 2/5дм меньше 5см
В шестом 4мес. больше 2/12г