41 и 53
Пошаговое объяснение:
Сначала возьмем наименьшее простое число и подберем к нему такое наименьшее число, чтобы при умножении друг на друга получилось число, которое максимально близко к 2021. Берем простое число 3 и 677. Если их перемножить то получится 2031. Но сумма этих числе равна 677+3=680. Далее пробуем увеличить 3 на 5. И к 5 опять подбираем такое простое число, чтобы при умножении число, которое максимально близко к 2021. Это 409 (если будет число меньше то произведение тоже будет меньше 2021). 409*5=2045. И заметим что сумма 409+5=414. Так мы увеличиваем первое число и подбираем к нему такое число, чтобы при умножении друг на друга получилось число, которое максимально близко к 2021. Вот мы и дошли до пары 41 и 53. Произведение будет равно 2173, а сумма уже 94. Если мы возьмем 43 и 47 то произведение будет равно 2021, а по условию она должна быть больше.
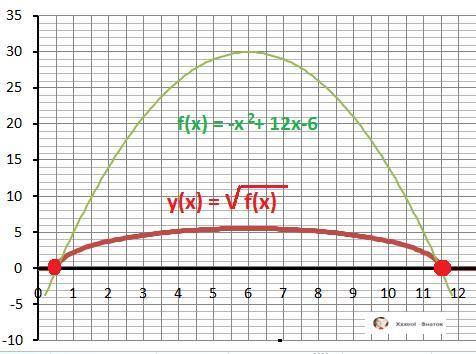
Дано: y(x) = √(-x²+12*x-6)
Найти: Значения Х при минимальных значениях y(x).
1. Функция y(x) = √f(x) - существует при f(x) ≥ 0.
2. Находим точки f(x)=0 - под знаком радикала.
Решение.
1) f(x) = - x² + 12*x - 6 - функция под знаком корня.
2) Решаем квадратное уравнение f(x) = 0, находим дискриминант и корни уравнения.
D = 12² - 4*(-1)*(-6) = 144-24 = 120 - дискриминант.
√D = √120 = √(2²*30) = 2√30.
x₁ = 6 - √30, x₂ = 6 + √30 - корни квадратного уравнения. Получили область определения функции y(x):
X∈[x₁;x₂] - ООФ y(x). Минимальные значения функция на границах отрезка.
Ymin(x)=0 при x₁ = 6 - √30, x₂ = 6 + √30 - ответ.
Дополнительно - графики функций - в приложении.
Максимальное значение функции y(x) равно:
Ymax(6) = √30 (≈ 5,48).
618 см3=618 000 мм3
2700см3=2,7 дм3 =0,0027м3
8530 мм3=8,53см3=0,00853 дм3
4 дм3 19 см3=4019 см3
3570дм3=3,57 м3=0.00000000357 км3