д²=а²+с², где а, в, с - ребра прямоугольного параллелепипеда, пусть с=16, тогда а²+в²=12², тогда д=√(12²+16²)=√(144+256)=√400=20
1. Скорость автобуса равна х км в час.
2. Так как расстояние равно скорость умноженная на время, найдем путь который автобус, он равен х * 2,1 = 2,1х км
3. Скорость автомобиля равна (х + 30) км в час.
4. Путь который автомобиль равен (х + 30) * 1,2 = 1,2 (х+30) км.
5. Поскольку нам известно что автобус и автомобиль равное расстояние составляем равенство, из которого находим скорость автобуса.
2,1х = 1,2 (х+30);
2,1х = 1,2х + 36;
2,1х - 1,2х = 36;
0,9х = 36;
х = 36 / 0,9;
х = 40 км в час.
6. Узнаем скорость автомобиля.
40 + 30 = 70 км в час.
ответ: Скорость автобуса 40 км в час, скорость автомобиля 70 км в час.
Пошаговое объяснение:
уравнение:
В первой бочке было x литров бензина, во второй 682-x литров.
Из первой бочки взяли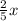 
л бензина, в ней осталось 
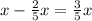л бензина.
Из второй бочки взяли 
л бензина, в ней осталось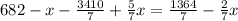 
л бензина.
В обеих бочках бензина стало поровну, то есть
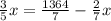
Умножим обе части уравнения на 35:
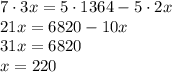
В первой бочке было 220 л бензина, во второй 682-220 = 462 литра.
система уравнений:
В одной бочке было x л бензина, во второй y л. Всего 682 л.
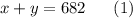
Из первой бочки взяли 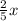л бензина, в ней осталось 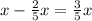л бензина.
Из второй бочки взяли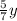 
л бензина, в ней осталось 
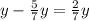л бензина.
В обеих бочках бензина стало поровну
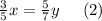
Составим и решим систему уравнений (1) и (2):
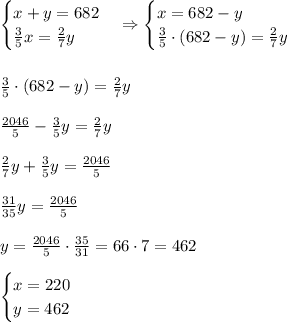
ответ: в первой бочке было 220 л бензина, во второй 462 л.
ответ: 20.
решение:
для этого применим теорему пифагора: сумма квадратов катетов (остальные стороны треугольника) равна квадрату гипотенузы (самая длинная сторона в прямоугольном треугольнике, находящаяся напротив угла в 90° градусов).
в данном случае роль катетов будут играть боковое ребро (16) и диагональ основания (12).
возводим их в квадрат, складываем и находим корень из суммы:
√(12² + 16²) = √(144 + 256) = √400 = 20.