ответ: Рома танцевал, Миша, Юра, Саша пели
Пошаговое объяснение:
Найдем кто из мальчиков танцевал
Рассмотрим Мишу, если Миша танцевал тогда Рома вместе с Сашей и Юрой пели, но так как в условии сказано что Рома не может показывать одинаковые номера с Сашей и Юрой, значит это не Миша
Если танцевал Юра, тогда Рома, Миша и Саша пели, что тоже не соответсвует условию задачи, потому что Рома и Саша не показывают одинаковые номера.
Если танцевал Саша, тогда Рома, Миша и Юра пели, что тоже не соответсвует условию задачи, потому что Рома и Юра не показывают одинаковые номера.
Значит танцевал Рома, тогда Миша, Юра и Саша пели. Все условия соблюдены.
Площадь квадрата равна квадрату его стороны.
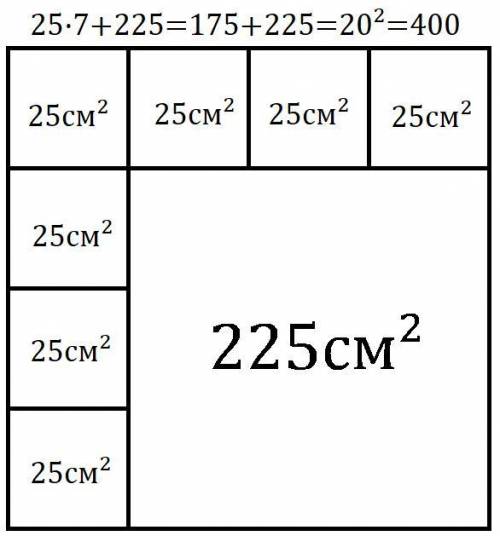
Тогда сторона маленького квадрата √25 = 5 см. У 7 из 8 квадратов сторона имеет целую длину (5см), поэтому сторона 8го квадрата тоже целая значит, длина листа бумаги целая.
Пусть сторона неизвестного квадрата n см, а длина листа L см.
Тогда распишем площадь листа: L² = 7·25+n² см².
Решим уравнение в целых числах.
L²-n² = 7·5·5
(L-n)(L+n) = 7·25 = 35·5
L и n это положительные целые числа, при этом L>n, поэтому множители левой части уравнения являются натуральными числами. L-n < L+n.
Рассмотрим два случая.
1.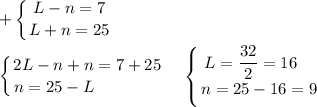
Если длина квадратного листа 16см и мы разрезали его на квадраты, то 16см можно записать, как сумму сторон разрезанных квадратов. Но не получится т.к. 5+5+5<16; 5+5+5+5>16; 5+5+9>16; 5+9<16.
Этот вариант отпадает.
2.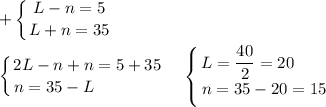
Заметим, что длину листа (20см) можно записать, как 5+15 см. Поэтому этот вариант реализуется.
15см - сторона оставшегося, 8го квадрата, тогда его площадь 15² = 225 см².
ответ: 225.
из второго уравнения y=52-x
x/(52-x)<3/5
x<3/5(52-x)=156/5-3/5x
x+3/5x<156/5
8/5x<156/5
8x<156
x<39/2=19,5
x (числитель дроби ) - положительное целое, меньшее 19,5. ответ : таких дробей 19