Формула Эйлера для многогранников.
Пусть В — число вершин выпуклого многогранника, Р — число его ребер и Г — число граней. Тогда верно равенство В+Г=Р+2.
Октаэдр - многогранник с 8 гранями. (Грани- треугольники)У него 6 вершин и 12 ребер.
8+6=12+2. Формула Эйлера верна.
Додекаэдр - многогранник, состоящий из граней- пятиугольников.Этих граней 12.У него 30 ребер и 20 вершин.
20+12=30+2 Формула Эйлера верна.
Икосаэдр - многогранник, состоящий из 20 граней-треугольников.
У него также, как и у додекадра,
30 ребер и 20 вершин.
20+12=30+2 Формула Эйлера верна.
40%, 35,7%, 120%
Пошаговое объяснение:
Для нахождения процентного соотношения
Надо составить с начало простое отношение
(В 6А 30 учеников, из них 12 учатся на отлично.)
Значит 12 частей из 30 и тоже самое со вторым.
И потом умножить его на 100%
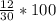
Дальше делаем обыденный действия.
Сокращаем при возможности дробь. (Разделить на одно число и числитель и знаменатель)
Первую делим на 6 потому что 12 и 30 делятся на 6.
Вторую делим на 2 потому что 10 и 28 делятся на 2.
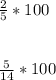
И наконец то умножаем. (Не буду расписывать надеюсь умеешь) )
Выходит что:
В 6A отличников 40%
В 6Б отличников 35.7% ≈ 36%
Теперь найдем отношение числа отличников 6А к числу отличников 6Б
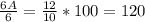
120%
%
%
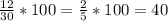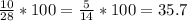12/10 · 100 = 120%
Выучи тему!
