Вначале заметим, что:
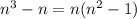
Докажем, что нечетное число в квадрате всегда дает остаток 1 при делении на 8 (поэтому, если отнять 1, то получится число, делящееся на 8):
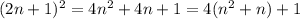
Данное число (если отнять 1) делится на 4 по разложению и еще на 2, так как n²+n по-любому четное (нечет. + нечет. = чет.). И: 4*2=8.
То есть, второй множитель, и, тогда, само число делится на 8. И нужно доказать, что оно еще должно делиться на 3.
1. Если n кратно трем, то задача решена: один множитель кратен 3, и, тогда, само произведение.
2. n не делится на 3. Докажем, что квадрат числа (если оно не делится на 3 и имеет остатки либо 1, либо 2) всегда дает остаток 1 при делении на 3 (и если от него отнять 1, то получится число, делящееся на 3):
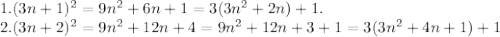
Итого: если число делится и на 3, и на 8, то оно делится на 3*8=24, что и требовалось доказать!
то голубой х+12
отрезали х+12-16=(х-16)*3
или так 3*(х-16)=х+12-16
3х-48=х-4
3х-х=48-4
2х=44
х=44/2
х=22это белая
а голубой х+12=22+12=34 первоначально