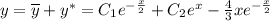НОД - это наибольшее натуральное число, на которое делятся без остатка два числа a и b.
Как найти НОД?
Пример: НОД (120; 36)
Для того чтобы найти НОК нужно разложить числа на простые множители:
120 = 2*2*2*3*5 = 2³*3¹*5¹
36 = 2*2*3*3 = 2²*3²
Надо найти наименьшие степени у чисел
Я выделил числа.
Нужно умножить выделенные числа: 2²*3¹ = 12
НОД (120; 36) = 12
Как найти НОК?
НОК - это наименьшие общие кратное двух натуральных чисел a и b.
Проще говоря число кратное как a, та и b.
Пример: НОК (60; 75)
Для того чтобы найти НОК нужно разложить числа на простые множители:
75 = 3*5*5 = 3¹*5²
60 = 2*2*3*5 = 2²*3¹*5¹
Надо найти наибольшие степени у чисел:
Нужно умножить выделенные числа: 3¹*5²*2² = 300
НОК (60; 75) = 300
ГЛАВНОЕ НЕ ЗАБЫТЬ ЧТО В НОД МЫ ИЩЕМ НАИМЕНЬШИЕ СТЕПЕНИ, А В НОК НАИБОЛЬШИЕ.
Удачи на контрольной)
Для начала нужно решить соответствующее линейное однородное дифференциальное уравнение, выполнив замену 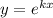 .
.
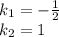
Общее решение однородного диф. уравнения: 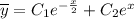 .
.
Рассмотрим функцию 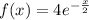 . Здесь
. Здесь 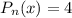 , где
, где 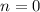 ,
, 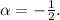 Сравнивая
Сравнивая 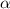 с корнями характеристического уравнения и принимая во внимая, что
с корнями характеристического уравнения и принимая во внимая, что
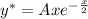
Определим первые две производные функции частного решения и подставляем в исходное дифференциальное уравнение одновременно разделив обе части на 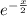 .
.
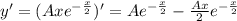
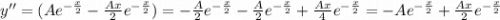
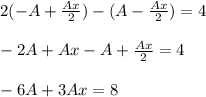
Приравниваем коэффициенты при степенях x
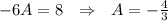
Общее решение линейного неоднородного дифференциального уравнения ищем как сумму общего однородного диф. уравнения и частного решения