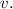 Тогда скорость Феди равна
Тогда скорость Феди равна 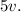 Когда Федя догоняет Соню, их скорость сближения равна
Когда Федя догоняет Соню, их скорость сближения равна 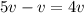 (вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения. Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.
(вычитаем, поскольку Соня уходит от догоняющего её Феди, тем самым, как бы мешая ему себя догонять). Когда Федя в очередной раз обгоняет Соню, его удалённость от Сони, которую он встретит в будущем, в следующем месте обгона, составляет как раз один круг. За время, пока Федя доедет до нового обгона Сони, Соня пройдет по круговой дорожке в 4 раза меньшее расстояние, поскольку её скорость в 4 раза меньше скорости сближения. Из этого и следует, что за время между двумя очередными последовательными встречами, которые разделяют участников движения расстоянием в один круг, Соня проходит только четверть круговой дорожки. Значит за 4 дополнительные встречи (после первой начальной) она и пройдёт полный круг. Т.е. всего существует 4 места, в которых малыш Федя обгоняет Соню на ходулях.
Тут решение лучше показать таблицей. 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 1 z x x x x x x x x x x x x x x 2 z x x x x x x x x x x x x x 3 z x x x x x x x x x x x x 4 z x x x x x x x x x x x 5 z x x x x x x x x x x 6 z x x x x x x x x x 7 z x x x x x x x x 8 z x x x x x x x 9 z x x x x x x 10 z x x x x x 11 z x x x x 12 z x x x 13 z x x 14 z x 15 z Всего игр может быть - сочетание 2 из 15 - то есть 15!/2!*13! = 105 Это в случае, если в турнире шахматист играет со своим противником только один раз, ну и ещё не забудем, что с самим собой он не играет, скорее всего =) Допустим, первый играет семь партий со 2,3,4,5,6,7,8. Тогда, они, в свою очередь, тоже играют по семь между собой.(то есть игроки 1-8 играют каждый между собой по семь игр). У нас тогда остаются ещё 7 человек. 9 играет с 10, 11, 12, 13, 14, и 15. Но на семёрку это не тянет. Поэтому с 15 шахматистами этого случится не может. А вот с 16 смогло бы) Таблицу тут необязательно рисовать, но я думал, что задача будет посложнее) так шо нарисовал.