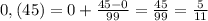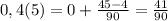![1)\; \int \frac{lnx\cdot dx}{x\cdot \sqrt{1+lnx}}=\int \frac{lnx\cdot \frac{dx}{x}}{\sqrt{1+lnx}}=[\ t=lnx,\; dt=\frac{dx}{x}\, ]=\\\\=\int \frac{t\cdot dt}{\sqrt{1+t}}=[\, z=\sqrt{1+t},\; z^2=1+t,\, t=z^2-1,\, dt=2z\, dz\, ]=\\\\=\int \frac{(z^2-1)\cdot 2z\, dz}{z}=2\int (z^2-1)\, dz=2(\frac{z^3}{3}-z)+C=\\\\=\frac{2}{3}\sqrt{(1+lnx)^3}-2\sqrt{1+lnx}}+C](/tpl/images/0370/0067/defcd.png)
![2)\; \int \frac{sinx\cdot cos^3x\, dx}{1+cos^2x}=[\, t=cosx,\, dt=-sinx\, dx\, ]=\\\\=-\int \frac{t^3\cdot dt}{1+t^2}=-\int (t-\frac{t}{1+t^2})\, dt=-\int t\, dt+\frac{1}{2}\int \frac{2t\, dt}{1+t^2}=\\\\=-\frac{t^2}{2}+\frac{1}{2}\int \frac{d(1+t^2)}{1+t^2}=-\frac{cos^2x}{2}+\frac{1}{2}ln|1+t^2|+C=\\\\=-\frac{cos^2x}{2}+\frac{1}{2}ln(1+cos^2x)+C](/tpl/images/0370/0067/733c3.png)
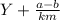 , где Y - количество целых, а - все цифры после запятой, включая цифры периода (если после запятой идет ноль он отбрасывается. b - все цифры стоящие после запятой, но до периода (ноль после запятой, аналогично а отбрасывается). к - количество цифр 9 равное количеству цифр в периоде, m - количество 0 равное количеству цифр, стоящих после запятой, но до периода. km - это не k*m, а просто количество 9 и 0 записанных рядом (k и m)
, где Y - количество целых, а - все цифры после запятой, включая цифры периода (если после запятой идет ноль он отбрасывается. b - все цифры стоящие после запятой, но до периода (ноль после запятой, аналогично а отбрасывается). к - количество цифр 9 равное количеству цифр в периоде, m - количество 0 равное количеству цифр, стоящих после запятой, но до периода. km - это не k*m, а просто количество 9 и 0 записанных рядом (k и m)