Пошаговое объяснение:
если 12 подарков, и два соседних подарка отличаются на 1, то получим 6 пар подарков, в каждой из которой один подарок четное кол-во конфет, другой - нечетное. т.е. получили 6 подарков с четным кол-вом конфет, и 6 подарков с нечетным кол-вом. (это можно наглядно увидеть, например, на циферблате часов - 1,2 ; 3,4; 5,6; 7,8; 9,10; 11,12 - вот 6 пар и в каждой по одному четному и одному нечетному, и каждые соседние отличаются на 1)
поехали дальше
если сложить все конфеты в 6ти подарках с четным количеством конфет, то получим в сумме четное количество конфет (например, 2+4+6+...+12 = 42 (эти цифры, кстати, могут просто считаться множителями для количества конфет в подарках с четным количеством конфет) )
и, если сложить конфеты в 6ти подарках с нечетным количеством конфет, то опять же получим количество конфет четное. (1+3+5+7+9+11 = 36)
т.е. для того, чтобы разложить конфеты по условию, нужно иметь общее четное количество конфет. а у нас их - нечетное
значит, не получится так разложить...
№ 4. x ≤ 0.75
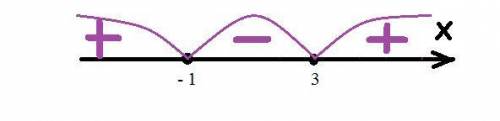
№ 5. ( - ∞; - 1 ] ∪ [ 3; + ∞ )
Пошаговое объяснение:
№ 4. 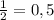
Тогда выражение имеет вид:
(0,5)^ (2*x) ≥ (0.125) ^ (1/2)
(0.5) ^ (2*x) ≥ ((0.5)^3)^(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3*(1/2)
(0.5) ^ (2*x) ≥ (0.5) ^ (3/2)
(0.5) ^ (2*x) ≥ (0.5) ^ 1.5
Т.к. 0,5 < 1, то имеем:
2 * х ≤ 1.5
x ≤ 1.5 / 2
x ≤ 0.75 или иначе записать можно так х ≤ 
№ 5. 7 ^ (x ^ 2) * 49 ^ ( - x) ≥ 343
7 ^ (x ^ 2) * 7^2^ ( - x) ≥ 7 ^ 3
7 ^ (x ^ 2) * 7^ ( - 2 * x) ≥ 7 ^ 3
7 ^ ((x ^ 2) + ( - 2 * x)) ≥ 7 ^ 3
7 ^ (x ^ 2 - 2 * x) ≥ 7 ^ 3
Т.к. 7 > 1, то запишем так:
x ^ 2 - 2 * x ≥ 3
Решим получившееся квадратное неравенство.
x ^ 2 - 2 * x = 3
x ^ 2 - 2 * x - 3 = 0
D = 16
x1,2 = (2±4)/2
x1 = 3 и x2 = -1
Решим методом интервалов.
( - ∞; - 1 ] ∪ [ 3; + ∞ )