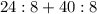
 повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение:
повторяется, поэтому вынесем это действие за скобку. Получим такое числовое выражение: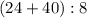
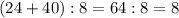 В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на
В ответе у нас получилось целое число. Значит можно считать утверждение "если каждое из двух чисел делится на  , то и их сумма делится на
, то и их сумма делится на  .
.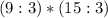
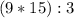
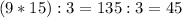
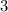 ,то их произведение делится на
,то их произведение делится на 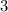 " доказанным.
" доказанным.
0^2=0, 1^2=1, 2^2=4, 3^2=9, остальные не подходят,т.к. в квадрате дают двузначное число.
Т.о. a,b,c могут быть только 0,1,4 или 9.
Рассмотрим условие "сумма цифр числа abcb равна числу, которое записывается как ab".
а+b+c+b=a+2b+c
ab=10a+b
a+2b+c=10a+b
c=9a-b
При "a,b,c могут быть только 0,1,4 или 9."
При ближайшем рассмотрении остается только два варианта
9=9*1-0, т.е. а=1, b=0,с=9
Это 1091
и
0=9*1-9
Это 1909
Из этих вариантов 1909>1091.
ответ: 1909
Если Вы, конечно, правильно написали условие abcb, а не abcd