В некотором царстве, а точнее царстве Математики, было государство Десятичных дробей. На вратах того государства висел герб, а на гербе было написано: “Казнить нельзя помиловать”. Тот, кто правильно ставил знак препинания проходил в это государство. Давайте и мы с вами попробуем правильно поставить запятую, чтобы продолжить повествование.
Жил там счастливый народ: десятичные дроби. Счастливый потому, что они легко и дружно справлялись с любой задачей
Много молодых царевичей сваталось к Марье Запятой, да уж больно сложные задания давала она им в качестве испытания. И каждый молодой принц уходил ни с чем, потому что не мог решить задачи, предложенные Марьей Запятой.
Но вот однажды появился Иван-удалец из государства Обыкновенных дробей, которому уж очень она приглянулась. Решил он свою судьбу испытать. Бухнулся перед ней на колени и предложил ей руку и сердце.
Даже глазом не повела Марья Запятая, но предложила ему испытание.
Она сказала ему, что если он расставит ответы в порядке убывания, то получит в ответе пароль – имя великого математика древности.
Глянул тут Иван-удалец на первый пример 16,2+3,18=
Долго Иван не думал надо сложить в столбик
И уже никогда наш Иван не затруднялся в решении примеров на сложение и вычитание дробей. Он для себя сделал вывод. Как вы думаете какой?
Пошаговое объяснение:
I вариант решения
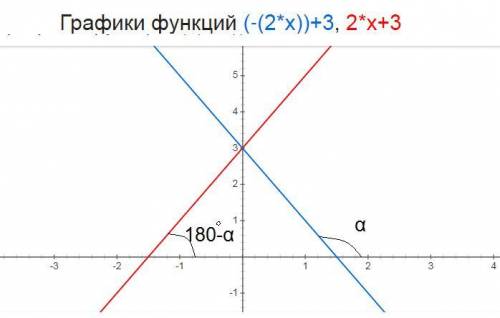
пусть прямая симметричная прямой y=-2x+3 имеет вид у=kx+b
найдем точки пересечения прямой y=-2x+3 с осями координат относительно оси ОУ
с осью ОХ у=0; -2x+3=0; 2x=3; x=1,5; (1,5;0)
с осью ОY x=0; y=3; (0;3)
так как прямые симметричны то
- они обе проходят через точку (0;3)
- симметричная прямая проходит через точку противоположную точке (1,5;0) точку (-1,5;0)
⇒ симметричная прямая проходит через точки (0;3) и (-1,5;0)
подставим координаты точки (0;3) в уравнение симметричной прямой у=kx+b координату точки (0;3)
получим 3=к*0+b; b=3
подставим координаты точки (-1,5;0) и значение b=3 в уравнение симметричной прямой у=kx+b получим
0=-1,5к+3 ; 1,5к=3; k=3/1,5=2
подставим b=1; k=2 в уравнение у=kx+b
у=2х+3
===============================================
II вариант решения - тригонометрический
так как прямые симметричны то их углы наклона к оси ОХ будут в сумме давать 180°
так как tg(180°-а)=-tga то угловые коэффициенты симметричных прямых будут к₁ и к₂ противоположными числами а значение b₁ и b₂ будут одинаковыми так как обе прямые пересекают ось ОУ в одной точке ⇒ к₂=-к₁=-(-2)=2; b₂=b₁=3
уравнение прямой симметричной прямой y=-2x+3 относительно оси ОУ
у=2х+3
128+24=152
ответ:на 6