a=6 см
b=8 см
∠C= α = 60°
c-?
1) По теореме косинусов находим третью сторону с:
c² = a² + b² - 2ab·cosα
c² = 6² + 8² - 2 · 6 · 8 · cos60°
c² = 36 + 64 - 2 · 6 · 8 · ¹/₂
c² = 100 - 48
c² = 52
с = 2√13 см
2) Находим площадь треугольника S через две стороны
a и b и углу между ними α по формуле:
a=6 см
b=8 см
∠C= α = 60°
c-?
1) По теореме косинусов находим третью сторону с:
c² = a² + b² - 2ab·cosα
c² = 6² + 8² - 2 · 6 · 8 · cos60°
c² = 36 + 64 - 2 · 6 · 8 · ¹/₂
c² = 100 - 48
c² = 52
с = 2√13 см
2) Находим площадь треугольника S через две стороны
a и b и углу между ними α по формуле:
Рассмотрим на двух примерах: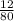 
и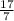 
1) Первым делом надо сократить дробь и сделать её правильной:
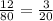
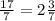
2) Затем есть два случая:
а) Знаменатель представляется в виде произведения степени двойки на степень пятёрки
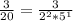
Домножаем числитель и знаменатель на нужную степень двойки/пятёрки, чтобы в знаменателе оказалась степень десятки
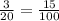
Переводим в десятичную дробь: записываем числитель, ставим запятую перед n-ной слева цифрой, где n - степень десятки в знаменателе (в нашем случае 2), при надобности дописываем необходимое количество нулей:
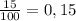
б) Знаменатель не представляется в виде произведения степени двойки на степень пятёрки (делится на простое число, не равное двум или пяти, в нашем случае - 7)
В таком случае, сделав дробь снова неправильной (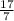) надо просто делить в столбик числитель на знаменатель, но предварительно поставив после числителя запятую и несколько нулей. Затем производит деление в столбик до тех пор, пока в вычитаемом (после приписывания нуля) не окажется то число, которое до этого уже было вычитаемым, когда уже приписывали нули после запятой:
_1 7,0 0 0 0 0 0 0 0 | 7
1 4 | 2,428571...
_3 0 <-- это число повторится
2 8
_2 0
1 4
_6 0
5 6
_4 0
3 5
_5 0
4 9
_1 0
7
3 0 <-- вот оно
С первого появления этого вычитаемого (включительно) до второго (не включительно) и будет период: В данном случае, когда первый раз появилось 30 (повторившееся вычитаемое), мы записали четвёрку (в данном случае она сразу после запятой, но так будет не всегда). Она - первая цифра в периоде. Когда во второй раз появилось 30 - мы (начиная с той четвёрки) записали 428571. Значит, это и есть период, т.е.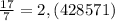 
На 1-м отрезке своего пути (вниз на 1м) жук находился внутри окружности, то есть на расстоянии, меньшем радиуса R = 2м .
На 2-м отрезке пути он полз от точки с координатами (0; -1) вправо по прямой у = -1. Здесь может быть пересечение с окружностью, которое найдём из уравнения х² + 1 = 4 → х² = 3 → х = +- √3 . корень +√3 не подходит, потому что жук полз вправо, то есть в сторону отрицательных х-ов. Остаётся х = -√3. то есть в точке с координатами (-√3; -1) жук ПЕРВЫЙ РАЗ находился на расстоянии 2м от точки О.
Дальше жук пополз вверх от точки с координатами (-2; -1) по прямой х = -2 . Подставим в уравнение окружности и получим 4 + у² = 4 → у = 0. То есть жук коснулся окружности в точке с координатами (2; 0) и ВТОРОЙ РАЗ находился на расстоянии 2м от точки О.
Дальше жук пополз от точки с координатами (-2; 2) вправо в по прямой у = 2. Подставив это значение в уравнение окружности, получим х² + 4 = 4 → х = 0. Следовательно, в точке с координатами (0; 2) жук ТРЕТИЙ РАЗ находился на расстоянии 2м от точки О.
Дальше жук опять повернул направо и пополз вниз по прямой х = 2. Подставим это значение в уравнение окружности и получим 4 + у² = 4 → у = 0 . В этом . Итак, ЧЕТВЁРТЫЙ РАЗ жук находился на расстоянии 2м от точки О в точке с координатами (2; 0) .
ответ: Получается, что всё же жук находился на расстоянии 2 м от точки О ЧЕТЫРЕ РАЗА