Пошаговое объяснение:
получить достоверные размеры прямоугольника нет возможности. Покажем последовательное решение данной задачи
1. Измерь линейкой размеры прямоугольника.
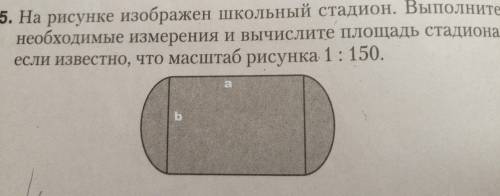
2.Стадион состоит из прямоугольника и двух полукругов с диаметром, который равен стороне прямоугольника.
Два полукруга это круг
3. Находим площадь прямоугольника S=a*b, a и b получим в процессе измерения линейкой. Масштаб 1: 150 показывает , что 1 см на плане равен 150 см на местности. Умножим размер a и b на 150 и получаем а*150=150а и b*150=150b это фактические размеры на местности в см
4.Находим площадь круга S=πr²=π*(d/2)²
d=b, а значит на местности d=150b/2 ширина прямоугольника
S=πr²=π*(150b/2)²
5. Площадь стадиона будет равна сумме площади прямоугольника и площади круга
S стад.=S прямоуг.+ S круга= 150a*150b+π* (150b/2)²
рисунок во вложении
Представим 2 прямоугольника. a -короткая и b-длинная стороны.По условию мы имеем разные периметры,а значит прямоугольники были поделены вдоль и поперек соответственно, т.к в противном случае периметры (P1 и P2) ,были бы одинаковы.
Итак имеем:, прям-к поделенный вдоль=> P1=2*((a-n)+n)+4b=50, где n это дельта(разница) каждой из сторон a; (a-n)-второй отрезок делимой стороны. соответственно P2 это прям-к поделенный поперек=4a+2((b-k)+k)=40, где K=дельте каждой из сторон b, P1>P2, т. к 4b>4a .Упрощаем:
P1=2(a+2b)=50; P2=2(2a+b)=40. Имеем систему из 2 уравнений, выражаем a из 1 уравнения и подставляем результат во 2.
1) a+2b=25
2) a=25-2b
3) 2((2(25-2b))+b)=40
4) 2(50-3b)=40
5) 100-6b=40
6) 60=6b
7) b=10
8) a=25-20
9) a=5
По формуле нахождения периметра прямоугольника P=2(a+b) => общий периметр=P0 = 2*15=30
ответ: P0=30см.
=349/75=4 49/75
6 1/12+1/18=73/12+1/18=219/36+2/36=
=221/36=6 5/36
5 3/10+11/15=53/10+11/15=159/30+22/30=
=181/30=6 1/30
9 5/24+35/36=221/24+35/36=663/72+70/72=
=733/72=10 13/72