На сколько минут дольше длится футбол, чем баскетбол, если в игре в футбол 2 тайма по 45 минут а в игре баскетбол 2 тайма по 20 тайма решения

👇

Увидеть ответ

Ответ:

EvdokiaNi

23.05.2023

2*45=90 МИНУТ 2*20=40 МИНУТ

4,7(78 оценок)

Открыть все ответы

Ответ:

osadchevasasha

23.05.2023

А1.

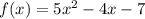
f(x) = 5x^2 - 4x - 7

Найдём производную данной функции.

$f'(x) = \left(5x^2)' - (4x)' - 7' = 5\cdot 2x - 4\cdot 1 - 0 = \bf{10x - 4}$

Найдём нули производной.

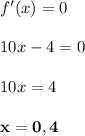
$f'(x) = 0\\\\10x - 4 = 0\\\\10x = 4\\\\\bf{x = 0,4}$

Определим знак производной на каждом промежутке.

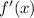
- + f'(x)

---------------------------------- $\bullet$ ----------------------------------> x

0,4

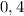
Функция возрастает там, где её производная положительна. А значит, она возрастает на промежутке 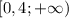$[0,4; +\infty)$ . Из перечня ответов полностью в этот промежуток входит только $\bf{(1;\ 12)}$ .

ответ: 3.

А2.

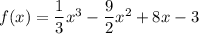
$f(x) = \dfrac{1}{3}x^3 -\dfrac{9}{2}x^2 + 8x - 3$

Найдём производную данной функции.

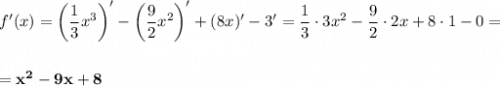
$f'(x) = \left(\dfrac{1}{3}x^3\right)' - \left(\dfrac{9}{2}x^2\right)' + (8x)' - 3' = \dfrac{1}{3}\cdot 3x^2 - \dfrac{9}{2}\cdot 2x + 8\cdot 1 - 0 =\\\\\\= \bf{x^2 - 9x + 8}$

Найдём нули производной.

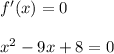
$f'(x) = 0\\\\x^2 - 9x + 8 = 0$

По теореме Виета:

$\begin{equation*}\begin{cases}x_1x_2 = 8\\x_1 + x_2 = 9\end{cases}\end{equation*}\ \ \ \ \ \Bigg| x = 1; x = 8$

Определим знак производной на каждом промежутке.

+ - + f'(x)

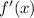
-------------------- $\bullet$ ----------------------- $\bullet$ --------------------> x

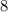
Функция убывает там, где её производная отрицательна. В нашем случае, на промежутке $\bf{[1; 8]$ . Ему соответствует вариант номер 2.

ответ: 2.

А3.

В точках минимума функция из убывания переходит в возрастание. На данном графике 4 такие точки (см. вложение).

ответ: 1.

А4.

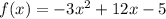
f(x) = -3x^2 + 12x - 5

Найдём производную данной функции.

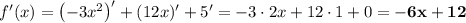
$f'(x) = \left(-3x^2\right)' + (12x)' + 5' = -3\cdot 2x + 12\cdot 1 + 0 = \bf{-6x + 12}$

Найдём нули производной.

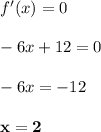
$f'(x) = 0\\\\-6x + 12 = 0\\\\-6x = -12\\\\\bf{x = 2}$

Точки максимума соответствуют точкам смены знака производной с плюса на минус. Проверим это, определив её знак на каждом промежутке:

+ - f'(x)

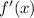
---------------------------------- $\bullet$ ----------------------------------> x

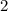
Полученные знаки соответствуют изложенному выше условию. Значит, 2 является точкой максимума функции.

ответ: 4.

А5.

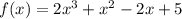
f(x) = 2x^3 + x^2 - 2x + 5

Найдём производную.

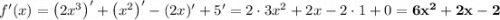
$f'(x) = \left(2x^3\right)' + \left(x^2\right)' - (2x)' + 5' = 2\cdot 3x^2 + 2x - 2\cdot 1 + 0 = \bf{6x^2 + 2x - 2$

Найдём нули производной.

$f'(x) = 0\\\\6x^2 + 2x - 2 = 0\\\\D = b^2 - 4ac = 2^2 - 4\cdot 6\cdot (-2) = 4 + 48 = 52\\\\x_1 = \dfrac{-b+\sqrt{D}}{2a} = \dfrac{-2+\sqrt{52}}{2\cdot 6} = \dfrac{2\sqrt{13} - 2}{2\cdot 6} = \dfrac{2\left(\sqrt{13} - 1\right)}{2\cdot 6} = \boxed{\bf{\dfrac{\sqrt{13}-1}{6}}}\\\\\\x_2 = \dfrac{-b-\sqrt{D}}{2a} = \dfrac{-2-\sqrt{52}}{2\cdot 6} = \dfrac{-\left(2+2\sqrt{13}\right)}{2\cdot 6} = \dfrac{-2\left(1 + \sqrt{13}\right)}{2\cdot 6} = \boxed{\bf{-\dfrac{\sqrt{13} + 1}{6}}}$

У производной нашлось 2 нуля. В то же время, производная равна нулю в точках экстремума графика функции. А значит, функция имеет две точки экстремума.

ответ: 1.

А6.

Точки максимума на графике производной соответствуют точкам смены знака производной с плюса на минус. На нашем графике это происходит в точке с абсциссой 3.

ответ: 2.

А7.

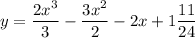
$y=\dfrac{2x^3}{3} -\dfrac{3x^2}{2} -2x+1\dfrac{11}{24}$

Найдём производную функции.

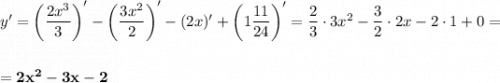
$y' = \left(\dfrac{2x^3}{3}\right)' - \left(\dfrac{3x^2}{2}\right)' - (2x)' + \left(1\dfrac{11}{24}\right)' = \dfrac{2}{3}\cdot 3x^2 - \dfrac{3}{2}\cdot 2x - 2\cdot 1 + 0=\\\\\\= \bf{2x^2 - 3x - 2}$

Найдём нули производной.

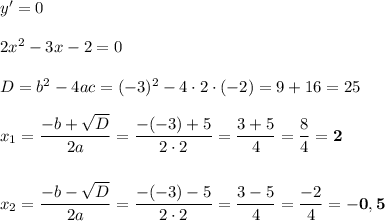
$y' = 0\\\\2x^2 - 3x - 2 = 0\\\\D = b^2 - 4ac = (-3)^2 - 4\cdot 2\cdot (-2) = 9 + 16 = 25\\\\x_1 = \dfrac{-b+\sqrt{D}}{2a} = \dfrac{-(-3) + 5}{2\cdot 2} = \dfrac{3 + 5}{4} = \dfrac{8}{4} = \boldsymbol{2}\\\\\\x_2 = \dfrac{-b-\sqrt{D}}{2a} = \dfrac{-(-3)-5}{2\cdot 2} = \dfrac{3 - 5}{4} = \dfrac{-2}{4} = \bf{-0,5}$

У производной нашлось 2 нуля. Найдём её знак на каждом промежутке.

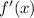
+ - + f'(x)

------------------ $\bullet$ ------------------- $\bullet$ -------------------> x

-0,5

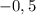
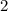
Точки минимума соответствуют точкам смены знака производной с минуса на плюс. Такой точке соответствует 2.

ответ: 4.

А8.

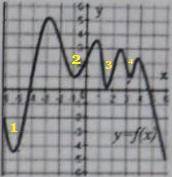
На заданном отрезке функция имеет одну точку максимума. Она соответствует значению функции, равному трём.

ответ: 2.

пожолуйста. Очень надо!Обязательно с решением.Матеша,производная.

4,5(9 оценок)

Ответ:

nky43939nky

23.05.2023

1. Первое фортепиано с возвратным механизмом для молоточков и возможностью играть с различным уровнем громкости было изготовлено около 1700 года итальянцем Бартоломео Кристофори, занимавшимся изготовлением клавесинов. Он усовершенствовал принцип их работы и создал несколько моделей фортепиано.

2. Слово «фортепиано» произошло от названия, данного Кристофори своему инструменту: «piano et forte» , что значит «тихо и громко»

3. Термин «рояль» был применен намного позже - через 77 лет.

4. Типичное фортепиано среднего размера имеет около 230 струн, каждая струна имеет натяжение около 70 кг, а суммарное натяжение – около 18 тонн.

5. Общее натяжение струн концертного рояля достигает 30 тонн.

6. Механизм, приводящий фортепиано в действие, называемый механика, имеет до 7500 деталей, каждая из которых участвует в процессе удара молоточка по струнам вследствие нажатия клавиши.

7. В процессе изготовления корпуса и механики фортепиано склеивают тысячи деревянных деталей; также используется войлок, оленья кожа, сталь, чугун, медь и другие металлы.

8. При изготовлении струн, помимо прочих материалов, использовали серебро, золото, стекло и шелк.

9. Исследования, проведенные в Германии, показали, что мозг пианистов обладает большей производительностью.

10. Независимые исследования определили более высокие показатели обучаемости в школе у детей, занимающихся фортепиано. Это относится к дисциплинированности, координации движения, навыкам поведения в обществе, более быстрому усвоению нового языка. Большую роль играет и удовольствие, получаемое в процессе создания музыки.

4,7(92 оценок)

Это интересно:

Образование-и-коммуникации

12.06.2021

Как составить план: секреты планирования на будущее...

Компьютеры-и-электроника

20.11.2020

Как создать простую таблицу стилей CSS с помощью Notepad...

Компьютеры-и-электроника

09.07.2020

Как уничтожить жесткий диск: советы и рекомендации...

13.09.2021