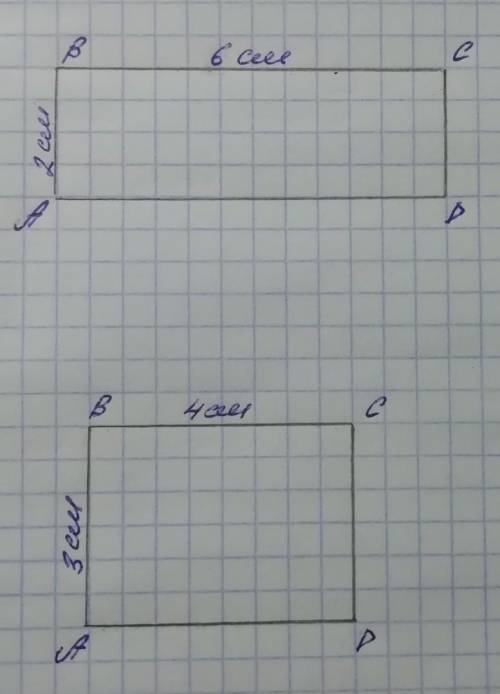
1-ый случай
1)Прямоугольник АВСD. S площадь АВСD = 12 см².
1)Прямоугольник АВСD. S площадь АВСD = 12 см². 2)Формула площади: S=a×b.
1)Прямоугольник АВСD. S площадь АВСD = 12 см². 2)Формула площади: S=a×b. 3)Подставляем числа 12=а×b => а = 6 см, b = 2 см => по формуле периметра прямоугольника P периметр ABCD = 2×(a+b) находим 16 см.
2-ой случай:
2-ой случай:1)Прямоугольник АВСD. S площадь ABCD = 12 см².
2-ой случай:1)Прямоугольник АВСD. S площадь ABCD = 12 см². 2)Формула площади: S=a×b
2-ой случай:1)Прямоугольник АВСD. S площадь ABCD = 12 см². 2)Формула площади: S=a×b3)Подставляем числа: 12=а×b => a = 6 см, b = 2 см => по формуле периметра прямоугольника P ABCD = 2×(a+b) находим 14 см.
ответ: 16 см, 14 см.
1)cos240 = cos(180 + 60)=cos (pi+pi/3)= -0.5, т.к. в 3 четверти косинус отрицателен
sin(2pi/3)=sin(120)=sin(180-60)=sin60=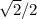
tg (-5pi/3)=-tg(300)=-tg(360-60)=-tg(-60)=tg60=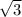
2)
a. 1-ctga*cosa*sina
1-(cos(a)/sin(a))*cos(a)*sin(a)= 1-cos²a= sin²a
б. sin (2pi+a)-cos(pi/2+a)=sina-(-sina)=2sina
4)sina/(1-cosa) + sina/(1+cosa)=(sin(1+cosa)+sina(1-cosa))/(1-cos^a)=2sina/sin^2a=2/sina
5)
cos^2 (a) * 1/ cos^2 (a) - sin^2 (a) = cos ^2 (a)
1-sin^2 (a) = cos^2 (a)
cos^2 (a) + sin^2 (a) = 1
чтд .
3) sin^2 (a) = 1 - cos^2 (a)
sin a= 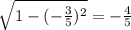
tg=sin/cos
tga=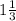
ctg=cos/sin
ctga=