1) 10*2=20(л)-сока заготовили.
2) 20-2=18(л)
5 часов
Пошаговое объяснение:
Первым действие рассчитает какую часть сосуда, кран A заполняет за 1 час.
Если принят сосуд за единицу, то за 1 час кран А заполнит 1/6 (1) сосуда.
Проделав тоже самое с кранами B и С, получим:
За 1 час кран В заполнит 1/8 (2) сосуда, а из крана С вытекает 1/12 (3) воды из сосуде.
В условии сказано, что "Первые два часа все три крана были открыты". То есть надо рассчитать какая часть сосуда будет заполнятся за час, если открыть три крана. Для этого мы суммируем значение (1) и (2) и отнимем от этого значение (3). Т.к вода из крана С(3) вытекает.
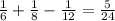
5/24 именно такая часть сосуда заполняется за 1 час, если открыть все 3 крана. За 2 часа соответственно в два раза больше:
5/24 * 2 = 5/12
Найдя количества воды, нам останется просто разделить на значение (3)
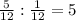
И мы получаем, что если первые два часа открыть все три крана, а затем закрыть краны А и В, то понадобиться еще 5 часов что бы вода полностью вытекла.
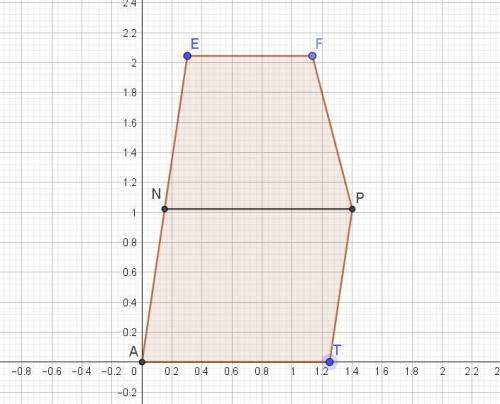
А) Построено сечение прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей середины рёбер A1B1, CC1, и вершину А (вложение 1).
Заданы точки А,Е и Р. За основу построения сечения принято свойство - в параллельных плоскостях линии сечения параллельны.
Проводим первый отрезок АЕ. В плоскости грани АА1В1В он проходит под углом к АА1, тангенс которого равен (1/2)/2 = 1/4. Под таким же углом к ребру СС1 проводим отрезок РТ. Точка Т разделит ребро CD основания на расстоянии (1/4) от точки С. Отрезок DT равен 1 – (1/4) = (3/4).
Далее проводим АТ по полученным точкам на основании АВСD и параллельно проводим под углом, тангенс которого равен (3/4) отрезок EF на верхнем основании. Этим определяется положение точки F, которая на ребре В1С1 выделит в отношении (1/2) / (3/4) = 4/6 = 2/3 отрезок B1F.
Отрезок FC1 = 1 – (2/3) = 1/3.
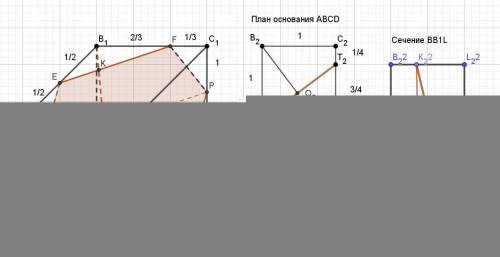
Б) Найдена площадь полученного сечения, из условия: ABCD-квадрат со стороной 1, а AA1=2 (вложение 2). Сечение дано в натуральную величину.
Оно разбито линией NP, параллельной АТ на 2 фигуры - трапецию и параллелограмм.
Положение точек Р и Т определено из подобия треугольников.
Так как точка Р находится на середине ребра СС1, то высоты трапеции и параллелограмма равны.
Длины оснований определяем по Пифагору.
АТ = √(1² + (3/4)²) = √(1 + (9/16)) = 5/4 = 1,25.
EF = √((1/2)² + (2/3)²) = √((1/4) + (4/9)) = √(9 + 16)/9) = 5/6.
Определяем наклонную высоту сечения. Для этого проводим секущую плоскость BB1L, перпендикулярную плоскости сечения.
Находим косинус угла D1FE: cos(D1FE) = (2/3) / (5/6) = 4/5, затем синус: sin(D1FE) = √(1 – (4/5)2) = 3/5.
Отсюда В1К = (2/3)*(3/5) = 2/5 = 0,4. Аналогично находим LQ = (3/4)*(3/5) = 9/20 = 0,45.
Отрезок BL = AT = 1,25, тогда проекция KQ на основание равна 1,25 – 0,4 – 0,45 = 0,4.
Наклонная высота сечения равна KQ = √(2² + 0,4²) = √4,16 ≈ 2,04.
Высоты частей сечения (трапеции и параллелограмма) равны по 2,04/2 = 1,02.
Находим площади трапеции S1 и параллелограмма S2 при условии NP = AT = 1,25.
S1 = ((EF + NP)/2)*1,02 = ((5/6)+1,25)/2)*1,02 = 1,041667*1,02 = 1,0625.
S2 = AT*1,02 = 1,25*1,02 = 1,275.
S = 1,0625 + 1,275 = 2,3375 кв.ед.