Для решения рассмотрим рисунок.
Из вершин тупых углом N и К опустим две высоты NH и КВ.
В прямоугольном треугольнике MNH, по теореме Пифагора определим дину катета МН.
МН = MN * Cos450 = 8 * √2 / 2 = 4 * √2 см.
В прямоугольном треугольнике КРВ, по теореме Пифагора определим дину катета РВ.
РВ = КР * Cos300 = 10 * √3 / 2 = 5 * √3 см.
Четырехугольник NКВН прямоугольник, так как NP параллельно НВ как основания трапеции, а NH параллельно КВ как высоты трапеции, тогда НВ = NK = 5 cм.
Определим длину основания МР. МР = НВ + МН + РВ = 4 * √2 + 5 + 5 * √3 ≈ 19,32 см.
Определим длину средней линии трапеции.
СД = (NK + MP) / 2 = (5 + 19,32) / 2 = 12.16 см.
ответ: Длина средней линии равна 12,16 см.
Представим эти числа в виде целых натуральных, что бы было удобнее, и лишь потом добавим к получившемуся результату добавим две запятые, поскольку в первом числе 1 число после запятой - 10,3, и во втором - 7, а как известно 1+1=2.
Я буду решать как бы "столбиком", это не отрицательнве числа!
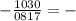
Мы от нуля не можем отнять семь, поэтому занимаем один десяток с разряда десятков, значит 20-17=3 и один в уме, этот один в уме мы добавляем к десяткам и получаем число, которое заканчивается на 13 в конце ( x x 1 3 ). Далее, отняв 8 от 10, мы получим 2, значит ответ будет ( 0 2 1 3 ). Добавляем те запятые сначала и получаем число 2,13
Пусть расстояние между поселком и городом S км
Тогда скорость велосипедиста S/5 км/ч, а скорость пешехода S/10 км/ч.
Скорость сближения
S/5+S/10 = 3S/10 км/ч
Тогда они встретятся через
S/(3S/10) = 10/3 ч = 3 1/3 ч = 3 ч 20 мин
2-й
Т.к. велосипедист тратит на весь путь в 10/5 = 2 раза меньше времени, то до встречи он пройдет 2.3 пути. а пешеход - 1/3.
Т.к. на весь путь велосипедист тратит 5 ч., то на 2/3 пути он потратит
5* 2/3 = 10/3 ч = 3ч 20 мин.