Решить . №1 средняя скороть автомобиля на трассе -u км/ч, а на проселочной дороге- в 3 раза меньше. запишите на языке. а) за 2 часа езды по трассе и 4 по проселочной дароге автомобиль проехал 260 километров. б) за 2 часа езды по
трассе автомобиль проехал на 60 км больше, чем за 4 часа по проселочной дороге. в) за 2 часа езды по трассе автомобиль проехал 120 км г)за 4 часа езды по проселочной дороге автомобиль проехал менее 150 км. №2 1)а=7см,b=12см. найти s 2) s=48
см в квадрате, а=12 см. найти b 3)s=144 в квадрате, b=12см. найти а 4)s=20 см в квадрате, а=8 см. найти р (периметр) №3 2л сиропа стоимостью 88 р. смешали с 20 л воды по цене 2р20коп за 1 л. найдите стоимость напитка иего цену.
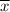 по векторам имеет вид:
по векторам имеет вид: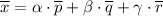
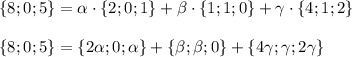
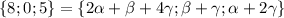
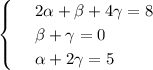




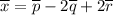
допустим, на проселочной дороге х км, тогда на трассе 3х, получим
а)2*3х+4х=260км
б)2*3х=4х-60
в)2*3х=120км
г)4х<150км
№2
1)а=7см,b=12см. Найти S=a*b=7*12=84см²
2) S=48 см в квадрате, а=12 см. найти b=S/a=48/12=4см
3)S=144 в квадрате, b=12см. Найти а=S/b=144/12=12см
4)S=20 см в квадрате, а=8 см. b=S/a=20/8=2,см5 Найти Р=2(a+b )=2(8+2,5)=21см
№3
88+20*2,2=132р стоимость напитка
132/(20+2)=6р цена 1 л