Пусть первая труба пропускает 
литров. Тогда вторая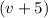 
л. Если мы вычтем из более производительной трубы мене производительную, то получим время, которое требуется второй трубе, когда первая труба уже заполнила резервуар. Это время по условию равно 10 мин:
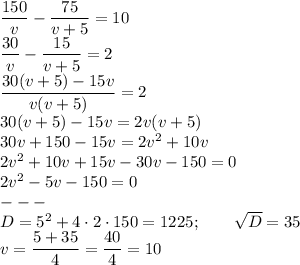
Второй корень явно отрицателен, поэтому он нам не подходит, т. к. скорость/производительность — величина положительная.
Тогда вторая труба по условию пропускает 10+5=15 л/мин
ответ: 1-я труба — 10 л/мин, 2-я труба — 15 л/мин.
Проверка: первая труба заполнит первый резервуар за 150:10=15 мин.
Вторая труба за 75:15=5 мин. Мы видим, что первый резервуар заполняется на 10 минут дольше, что и требовалось доказать.
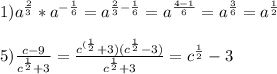
3)
√(5-x²)-3x=0
√(5-x²)=3x
Найдём ОДЗ (область допустимых значений):
а) Выражение под знаком квадратного корня не может быть отрицательным,значит.оно больше или равно 0.
в) В правой части не может стоять отрицательное значение,так как квадратный корень из числа есть число неотрицательное,значит,x≥0.
Решаем систему:
{5-x²≥0 {x²≤5 {-√5≤ x ≤ +√5 ⇒ ОДЗ : 0 ≤ x ≤√5
{3x≥0 {x≥0 {x≥0
Теперь,когда и правая,и левая части у нас положительные,можем возвести их в квадрат:
(√(5-х²)²=(3х)²
5-х²=9х²
9х²+х²=5
10х²=5
х²=0.5
х1=√0.5 >0, но <√5 -значит, х1 -корень уравнения
х2= -√0.5 -не удовлетворяет ОДЗ: 0 ≤ x ≤ √5
ответ: х=√0.5.
------------------------------------------------------------
Если вам удобнее проверить корни,подставив их значения в уравнение,то так тоже можно.
