Заданное уравнение х+√(16-х^2) = a представим так:
√(16-х^2) = -х + a.
Левая часть - уравнение полуокружности в положительной полуплоскости, правая - уравнение прямой, в котором параметр а соответствует ординате точки пересечения с осью Оу.
Возведём в квадрат.
16-х^2 = х²- 2aх + а².
Получили квадратное уравнение:
2х²- 2aх + (а² - 16) = 0.
Дискриминант D = 4a²- 4*2*(а² - 16) = -4а² + 128.
Уравнение имеет единственное решение, если дискриминант равен нулю:
-4а² + 128 = -4(а² - 32) = 0.
Отсюда а = +-4√2.
Но так как на промежутке а = (4...4√2) имеется 2 решения, а значение а = -4√2 выходит из области определения, то в ответ включаем:
-4 <= а < 4, а = 4√2.
1)
Приводим к общему знаменателю то, что в скобках:
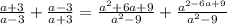
Записываем под общей чертой и упрощаем:
Делим получившуюся дробь на оставшуюся:
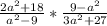
в числителе второй дроби можно превратить в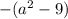 
и сократить полученные слагаемые:
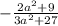
Выносим общие множители за скобки:
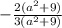
Упрощаем:
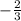
2)
Приводим к общему знаменателю то, что в скобках:
Записываем под общей чертой и упрощаем:
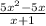
Делим получившуюся дробь на оставшуюся, вынося общие множители за скобки:
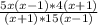
Упрощаем:
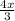
3)
Умножим дроби, вынося общие множители:
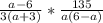
Знаменатель второй дроби превратим в -a(a-6)
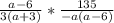
Запишем дроби под одной чертой и упростим их:
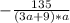
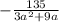
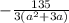
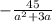
Вычтем из первой дроби вторую, приведя их к общему знаменателю:
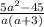
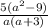
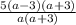
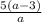
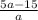
Найти НОД. (оформляется это обычно так, как в приложении выше)
1) Д(204) = 2 × 2 × 3 × 17,
Д (420) = 2 × 2 × 3 × 5 × 7;
НОД = 2 × 2 × 3 = 12.
2) Д(144) = 2 × 2 × 2 × 2 × 3 × 3,
Д(324) = 2 × 2 × 3 × 3 × 3 × 3;
НОД = 2 × 2 × 3 × 3 = 36.
3) Д(625) = 5 × 5 × 5 × 5,
Д(875) = 5 × 5 × 5 × 7;
НОД = 5 × 5 × 5 = 125.
4) Д(126) = 2 × 3 × 3 × 7,
Д(378) = 2 × 3 × 3 × 3 × 7;
НОД = 2 × 3 × 3 × 7 = 126.