Пошаговое объяснение:
Пошаговое объяснение:
5.36. -6(7 - x) = -8x - 7.
-42 + 6х = -8х - 7
6х+8х = -7 +42
14х = 35
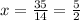
.5.37. 4(-3 + x) = 5x + 2.
-12 + 4х = 5х + 2
-12 - 2 = 5х - 4х
х = - 14
5.38 -5y + 19 = 2(2-6y).
-5y + 19 = 4 - 12y
-5y + 12y = 4 - 19
7y = -15
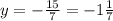
9 (14 - x) =-2x
9*14 - 9x = -2x
9*14 = -2x+9x
9*14 = 7x
x = 9*14 : 7 = 18
x= 18
4(-3 + x) = 5x + 2
-12+4x = 5x + 2
-12-2 = 5x - 4x
x = -14
-9(1 + 6x) = 6x - 37
-9 -54x = 6x - 37
-9+37 = 6x + 54x
28 = 60x
x = 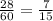
-6(7 - x) = -8x – 7
-42 + 6x = -8x -7
6x+8x = -7 + 42
14x = 35
x = 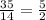
x = 2,5
-5y + 19 = 2(2-6y)
-5y + 19 = 4 - 12y
-5y +12y = 4 - 19
7y = - 15
y = 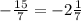
Продолжаем изучать деление. В данном уроке мы рассмотрим такие понятия, как НОД и НОК.
НОД — это наибольший общий делитель.НОК — это наименьшее общее кратное.Тема довольно скучная, но разобраться в ней нужно обязательно. Не понимая этой темы, не получится эффективно работать с дробями, которые являются настоящей преградой в математике.
Второй и третий довольны просты и дают возможность быстро найти НОД. Рассмотрим все три А какой применять на практике — выбирать вам.
Первый заключается в поиске всех возможных делителей двух чисел и в выборе наибольшего из них. Рассмотрим этот на следующем примере: найти наибольший общий делитель чисел 12 и 9.
льшим и общим делителем чисел 12 и 9 является число 3
Второй нахождения НОДТеперь рассмотрим второй нахождения наибольшего общего делителя. Суть данного заключается в том, чтобы разложить оба числа на простые множители и перемножить общие из них.
Пример 1. Найти НОД чисел 24 и 18
Сначала разложим оба числа на простые множители:
Теперь перемножим их общие множители. Чтобы не запутаться, общие множители можно подчеркнуть.
Смотрим на разложение числа 24. Первый его множитель это 2. Ищем такой же множитель в разложении числа 18 и видим, что он там тоже есть. Подчеркиваем обе двойки:
Снова смотрим на разложение числа 24. Второй его множитель тоже 2. Ищем такой же множитель в разложении числа 18 и видим, что его там второй раз уже нет. Тогда ничего не подчёркиваем.
Следующая двойка в разложении числа 24 также отсутствует в разложении числа 18.
Переходим к последнему множителю в разложении числа 24. Это множитель 3. Ищем такой же множитель в разложении числа 18 и видим, что там он тоже есть. Подчеркиваем обе тройки:
Итак, общими множителями чисел 24 и 18 являются множители 2 и 3. Чтобы получить НОД, эти множители необходимо перемножить:
2 × 3 = 6
Значит НОД (24 и 18) = 6
Третий нахождения НОДТеперь рассмотрим третий нахождения наибольшего общего делителя. Суть данного заключается в том, что числа подлежащие поиску наибольшего общего делителя раскладывают на простые множители. Затем из разложения первого числа вычеркивают множители, которые не входят в разложение второго числа. Оставшиеся числа в первом разложении перемножают и получают НОД.
Пример 1. Найти НОД чисел 28 и 16.
Нахождение НОД для нескольких чиселНаибольший общий делитель можно находить и для нескольких чисел, а не только для двух. Для этого числа, подлежащие поиску наибольшего общего делителя, раскладывают на простые множители, затем находят произведение общих простых множителей этих чисел.
Например, найдём НОД для чисел 18, 24 и 36
Разложим на множители число 18
Наименьшее общее кратное
Из предыдущего урока мы знаем, что если какое-то число без остатка разделилось на другое, его называют кратным этого числа.
Оказывается, кратное может быть общим у нескольких чисел. И сейчас нас будет интересовать кратное двух чисел, причем оно должно быть максимально маленьким.
Определение. Наименьшее общее кратное (НОК) чисел a и b — это наименьшее число, которое кратно a и b. Другими словами, это такое маленькое число, которое делится без остатка на число a и число b.
Определение содержит две переменные a и b. Давайте подставим вместо этих переменных любые два числа. Например, вместо переменной a подставим число 9, а вместо переменной b подставим число 12. Теперь попробуем прочитать определение:
Наименьшее общее кратное (НОК) чисел 9 и 12 — это наименьшее число, которое кратно 9 и 12. Другими словами, это такое маленькое число, которое делится без остатка на число 9 и на число 12.
Из определения понятно, что наименьшее общее кратное это наименьшее число, которое делится без остатка на 9 и на 12. Это наименьшее общее кратное требуется найти.
Для нахождения наименьшего общего кратного (НОК) можно пользоваться тремя Первый заключается в том, что можно выписать первые кратные двух чисел, а затем выбрать среди этих кратных такое число, которое будет общим для обоих чисел и маленьким. Давайте применим этотВ первую очередь, найдем первые кратные для числа 9. Чтобы найти кратные для 9, нужно эту девятку поочерёдно умножить на числа от 1 до 9. Получаемые ответы будут кратными для числа 9.
Второй нахождения НОКВторой заключается в том, что числа для которых ищется наименьшее общее кратное раскладываются на простые множители. Затем выписываются множители, входящие в первое разложение, и добавляют недостающие множители из второго разложения. Полученные множители перемножают и получают НОК.
Применим данный для предыдущей задачи. Найдём НОК для чисел 9 и 12.
Третий нахождения НОКЕсть и третий нахождения наименьшего общего кратного. Он работает при условии, что его ищут для двух чисел и при условии, что уже найден наибольший общий делитель этих чисел.
Данный разумнее использовать, когда одновременно нужно найти НОД и НОК двух чисел.
30*3=90
ответ:3