
ответ: min y = -3, max y = -1.
Пошаговое объяснение:
Находим производную.
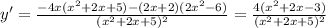
Приравниваем нулю множитель числителя с переменной.
Решаем уравнение x^2+2*x-3=0.
Ищем дискриминант:
D=2^2-4*1*(-3)=4-4*(-3)=4-(-4*3)=4-(-12)=4+12=16;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√16-2)/(2*1)=(4-2)/2=2/2=1;
x_2=(-√16-2)/(2*1)=(-4-2)/2=-6/2=-3.
Находим знаки производной в промежутках между критическими точками.
x = -4 -3 0 1 2
y' = -0,118343 0 0,48 0 -0,118343 .
Как видим, в точке х = -3 минимум функции, а в точке х = 1 - максимум.
Находим значения функции в этих точках.
у(-3) = (-2(9+3))/(9-6+5) = -24/8 = -3.
у(1) = (-2(1+3))/(1+2+5) = -8/8 = -1.
На заданном промежутке [-5; 1] значение функции у(1) = -1 является максимальным, а у(-3) =-3 минимальным.
у нас так
Пошаговое объяснение:
ответ Леонида верен, но нужно более серьезное обоснование.
Псть одно дерево дает n золотых монет. Возможны две модели поведения.
1. Буратино-Жадина. Хочет как можно быстрее получить как можно большую прибыль, поэтому каждый раз закапывает все золотые монетки. Во вторник он получит 5*n монет, в среду 5*n^2, и т. д. Если при этом выполнены условия задачи, то
5*n^2≤1992≤5*n^4
n^2≤398,4≤n^4
Решим в целых числах.
5≤n≤19
Таким образом он никогда не наберет 1992 монеты, потому, что 1992 не крано 5.
Это было очевидно с самого начала. Оценка n понадобится нам чуть позже.
2. Буратино-Маньяк. Ему не важно сколько он потратит дней. Он может закапывать любое число монет, если они у него есть, лишь бы когда-нибудь набрать ровно 1992. Пусть дерево дает урожай n монет. Сколько бы монет он не посадил, прибыль будет кратна n-1 (одну монету он тратит на выращивание дерева) . Чтобы достичь цели ему необходимо, чтобы 1992-5=1987 делилось на n-1
Но число (проверил по таблице) , значит, n=2 или n=1988
В первом случае он явно не укладывается в 5 дней (см. вариант 1).
Во втором случае он достигне резултата в первый же день.