а) Запишем уравнение в следующем виде: tg(x)dy(x)/dy-y(x)=2
dy(x)/dy=(2-y(x))*ctg(x)
Делим обе части на (2-y(x)):
(dy(x)/dy)/(2-y(x))=ctg(x)
Интегрируем обе части по Х:
инт((dy(x)/dy)/(2-y(x)))=инт(ctg(x)dx)
Получаем: lg(y+2)=lg(sinx)+C1
Т.к. lg(y+2)-lg(sinx)=lg((y+2)/sin(x)), то lg((y+2)/sin(x))=С1
(y+2)/sin(x)=е^C1
y=C1*(sin(x)-2)
б) Запишем характеристическое уравнение: 3*k^2-2*k-8=0
Корни этого уравнения k1=(2-корень(2^2-4*3*(-8)))/(2*3)=-8/6=-4/3
k2=(2+корень(2^2-4*3*(-8)))/(2*3)=2
Решение данного уравнения будет иметь вид e^k*x.
Общее решение: y=e^(-4*x/3)*C1+e^(2x/)*C2
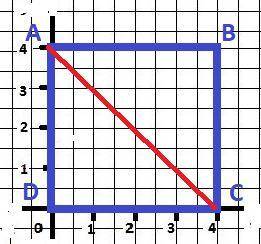
ДАНО: P= 16 см - периметр квадрата ABCD.
НАЙТИ: S(ABC) = ? - площадь треугольника.
РЕШЕНИЕ
Периметр квадрата по формуле:
Р = 4*а = 16 см
Находим сторону квадрата:
а = Р/4 = 16:4 = 4 см - сторона.
Начертили квадрат - рисунок в приложении.
1 см = 2 клетки в тетради. Обозначили вершины латинскими буквами. Провели диагональ квадрата АС .
ΔАВС = ΔADC - равные по двум сторонам и углу между ними, равнобедренные.
Площадь треугольника по формуле:
S(ABC) = 1/2*a*b = 1/2*a² = 4*4/2 = 8 см² - площадь треугольника - ОТВЕТ
Пошаговое объяснение:
Периметр - это сумма длин всех сторон.
Одна сторона равна 5 см.
Вторая сторона:
5 - 3 = 2 (см)
Найдем периметр:
5 + 2 + 5 + 2 = 14 (см)
ответ: периметр прямоугольника равен 14 см.