1. Пусть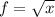 
, 
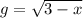. Заметим, что 
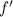и 
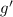монотонно убывают, значит, 
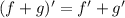функция монотонная, следовательно, имеет не более одного корня. Из этого следует, что у уравнения 
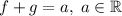не более двух корней.
2. Заметим, что если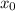 
является решением, то 
тоже. Очевидно, что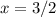 
является осью симметрии (причем единственной) графика 
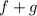. Иначе говоря, пара 
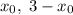исчерпывает все решения указанного уравнения, если таковые имеются. Значит, достаточно потребовать, чтобы 
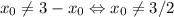. Итак, 
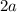пробегает область значения рассматриваемой функции, кроме того 
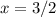, которому соответствует (это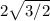 
).
3. Функция непрерывна, поэтому достаточно посмотреть на наименьшее и наибольшее значения. Наименьшее значение достигается в 0 (то есть значение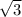 
, а наибольшее в 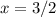. Получаем ответ: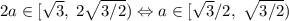 
6527.
Пошаговое объяснение:
Получились следующие числа : 1029,1092,1209,1290,1902,1920,2019,2091,2109,2190,2901,2910,9012,
9021,9102,9120,9201,9210. Числа расположены в порядке возрастания. Признак делимости натуральных чисел на 11 : число делится на 11 тогда и только тогда, когда разность между суммой цифр, стоящих на нечётных местах и суммой цифр, стоящих на чётных местах, делится на 11. В частности, эта разность может равняться 0, т. е. вышеуказанные суммы равны. Наша задача прибавить к каждому из этих чисел натуральное число, так, чтобы остаток от деления полученного числа на 11 не был равен 1. Будем прибавлять сначала самое маленькое натуральное число 1. 1029 + 1=1030. Остаток от деления на 11 равен 7. Подойдёт. Разность равна 4. До 11 не хватает 7.
1092+1=1093, разность равна 7. До 11 не хватает 4, т.е. остаток 4. Годится. 1209 + 1=1210. Разность равна 0. Число делится на 11. Остаток 0. 0 не равен 1. Подойдёт. 1290 + 1=1291. Разность равна 7. До 11 не хватает 4. Остаток 4. Берём. 1902 + 1= 1903. Разность равна 11. Делится на 11. Подойдёт. Это и будут первые 5 чисел в новом ряду. Сложим их : 1030+ 1093+1210+1291+1903=6527.
2)25+60=85кг-гвоздей было