1)как связаны между собой уравнения каждой строки? 9x-2x=84 (9-2)x=84 7x=84 6y+3y=486 (6+3)y=486 9y=486 какое свойство умножения здесь использовано? 2)реши самые простые из данных уравнений.будут ли корнями остальных уравнений найденные числа? проверь предложение: подставь числа . 3)реши уравнения. 19x-15x=96 5b+3b=456

👇

Ответ:

AnnaNazar07

18.03.2022

1) это распределительный закон умножения относительно сложения
a(b+c)=ab+ac
a(b-c)=ab-ac

Но применяется справа налево
ab+bc=a(b+c)
ab-bc=a(b-c)

самые простые - это последние в цепочке
7x=84
х=84:7
х=12
Проверим, подставим в данное уравнение
9·12-2·12=84
108-24=84 - верно

9y=486
у=486:9
у=54
Проверим, подставим в данное уравнение
6·54+3·54=486
324+162=486 - верно

Реши уравнения.
19x-15x=96
(19-15)х=96
4х=96
х=96:4
х=24

5b+3b=456
(5+3)b=456
8b=456
b=456:8
b=57

4,5(20 оценок)

Открыть все ответы

Ответ:

mironmashstem

18.03.2022

Пошаговое объяснение:

здесь не будем заморачиваться тройными интегралами. посмотрим на наши поверхности

1 страшная формула - это однополостный гиперболоид

две других - это плоскости

объем тела, содержащегося между плоскостями z = а и z = Ь, выражается формулой:

$\displaystyle \int\limits^a_b {S(z)} \, dz$ , где S (z) — площадь сечения тела плоскостью, перпендикулярной к оси ординат в точке z.

плоскость, перпендикулярная оси Оz, в точке с аппликатой z пересекает гиперболоид по эллипсу

запишем наш эллипс

$\displaystyle \frac{x^2}{16} +\frac{y^2}{9} =1+\frac{z^2}{16}$

теперь нам надо каноническое уравнение нашего эллипса

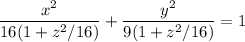
$\displaystyle \frac{x^2}{16(1+z^2/16)} +\frac{y^2}{9(1+z^2/16)}=1$

упростим

$\displaystyle \frac{x^2}{16+z^2} +\frac{y^2}{(9/16)(16+z^2)} =1$

площадь этого замечательного гиперболоида вычисляется по формуле

S=πab

у нас

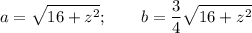
$\displaystyle a =\sqrt{16+z^2} ; \qquad b=\frac{3}{4} \sqrt{16+z^2}$

отсюда

S=π*(3/4)(16+z²)

вот, собственно, и все "загогулины"

остался только объем

$\displaystyle V=\frac{3}{4} \pi \int\limits^2_0 {(16+z^2)} \, dz = \pi \bigg (\frac{3}{4}*16z\bigg |_0^2+\frac{3}{4}*\frac{z^3}{3} \bigg |_0^2 \bigg )= \pi (2+24)=26\pi$

Вычислить объем тела, ограниченного поверхностями

4,4(89 оценок)

Ответ:

sasha13410

18.03.2022

№ 212.2 литра это два кубических дециметра. В одном дециметре 10 см, в 1-ом куб. дециметре 1000 см кубических. В 1 метре кубическом миллион см кубических. Нужно знать плотность керосина, это вроде 700 кг на метр кубический. 2000 см куб=0,002 метр куб. 0,002 умножить на 700 =1,4 кг.

№ 213.металлический кусок имеет объём 200 см кубических и массу 540 граммов. из какого металла этот кусок? какова его плотность?

№218.1,4*1*10^-3 и все это на плотность железа

№219.p = m/VОтсюдаV = m/p = 4 / 800 = 0.005 м³ - такой ёмкости нужна бутыль

№220.надо плотность нефти поделить на массу

№223.Если брать в среднем, 1 куб.метр песка весит 1,5 тонн.Значит в одном вагоне помещается 10 куб.метров песка.А для 400 000 куб.метров нужно 40 000 вагонов :
400 000 : 10 = 40 000

4,6(7 оценок)

Это интересно:

Хобби-и-рукоделие

26.07.2020

Как выращивать спирулину дома...

26.01.2022

Как помочь другу справиться с депрессией...

Дом-и-сад

28.11.2021

Как сделать небольшую септическую систему...

Здоровье

16.08.2022