Дано уравнение:
−2(x+1)2+(−5(x+1)((x2−x)+1)+3((x2−x)+1)2)=0
преобразуем:
Вынесем общий множитель за скобки
(x2−3x−1)(3x2−2x+4)=0
Т.к. правая часть ур-ния равна нулю, то решение у ур-ния будет, если хотя бы один из множителей в левой части ур-ния равен нулю.
Получим ур-ния
x2−3x−1=0
3x2−2x+4=0
решаем получившиеся ур-ния:
1.
x2−3x−1=0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с дискриминанта.
Корни квадратного уравнения:
x1=D−−√−b2a
x2=−D−−√−b2a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a=1
b=−3
c=−1
, то
D = b^2 - 4 * a * c =
(-3)^2 - 4 * (1) * (-1) = 13
Т.к. D > 0, то уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
x1=32+13−−√2
x2=32−13−−√2
2.
3x2−2x+4=0
Это уравнение вида
a*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с дискриминанта.
Корни квадратного уравнения:
x3=D−−√−b2a
x4=−D−−√−b2a
где D = b^2 - 4*a*c - это дискриминант.
Т.к.
a=3
b=−2
c=4
, то
D = b^2 - 4 * a * c =
(-2)^2 - 4 * (3) * (4) = -44
Т.к. D < 0, то уравнение
не имеет вещественных корней,
но комплексные корни имеются.
x3 = (-b + sqrt(D)) / (2*a)
x4 = (-b - sqrt(D)) / (2*a)
или
x3=13+11−−√i3
x4=13−11−−√i3
Тогда, окончательный ответ:
x1=32+13−−√2
x2=32−13−−√2
x3=13+11−−√i3
x4=13−11−−√i3
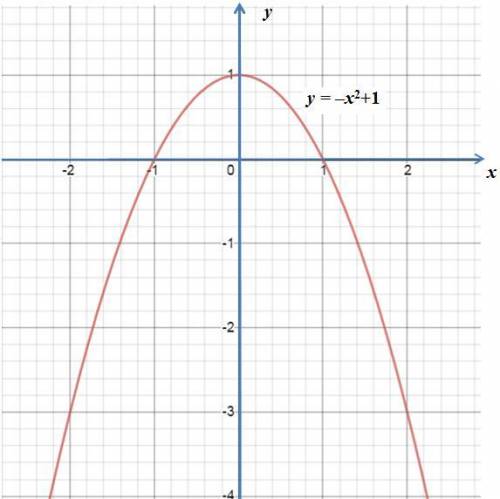
Дана функция: y = –x²+1 – парабола.
Определим абсциссу и ординату вершины параболы:
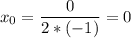
y₀ = y(x₀) = y(0) = –0²+1 = 1.
Определим нули функции:
y = 0 ⇔ –x²+1 = 0 ⇔ x² = 1 ⇔ x = ±1.
Так как перед x² коэффициент –1<0, то ветви параболы направлены вниз.
Чтобы определить, при каких значениях х функция принимает отрицательные значения, можно
использовать свойство параболы: так как y₀=1>0 и x₀=0∈[-1; 1], то на промежутке (-1; 1) функция принимает положительные значения, а в промежутках (–∞; –1) и ( 1; +∞) - отрицательные значения;
рассмотреть знак функции в промежутках (–∞; –1), (–1; 1), ( 1; +∞):
y = –x²+1 : – + –
------------------------(–1)--------------------(1)-----------------> x
Значит: в промежутках (–∞; –1) и ( 1; +∞) функция принимает отрицательные значения.
Для построения графика достаточно знать вершину и нули функции (график в приложении).
1. Смолистое дерево с вечнозеленой листвой, отличающееся ароматическим запахом. там лавры зыблются, там апельсины зреют. Пушкин.
2. чаще мн. То же, что лавровый венок, лавровая ветвь или листья, как символ победы, награды (см. лавровый; книжн. ритор.). Лаврами побед увиты, бойцы из чаши мира пьют. Пушкин. Венец терновый, увитый лаврами, надели на него. Лермонтов (о Пушкине).
3. перен., только мн. Успех, слава, триумф (книжн.). Пожинать, пожать лавры (см. пожать). почить на лаврах (см. почить). Видимо, лавры Дон-Кихота не дают спать нашим "левым" загибщикам. Сталин ("ответ товарищам колхозникам", 1930 г.). (Выражение: "чьи-н. лавры не дают спать кому-н.", означающее: кто-н. завидует чьему-н. успеху, идет из греч. истории - слова Фемистокла: "лавры Мильтиада не дают мне спать".);