29) 192
38) 6
Пошаговое объяснение:
29) Для арифметической прогрессии справедливо соотношение
Сумма членов с номерами 1 и n, равна сумме членов с номерами 2 и (n-1), равна сумме членов с номерами 3 и (n-2) и т.д. То есть если сумма номеров членов последовательности равна n+1, то равны и их суммы.
Ряд составленный из членов с номерами 3,6,9,...,3n это тоже арифметическая прогрессия значит равны суммы членов с такими номерами:
3 и 3n;6 и 3n-3;9 и 3n-612 и 3n-9То есть, если сумма номеров членов последовательности равна 3n+3, то равны и их суммы. А сумма всех членов последовательности от 3 до 3n с шагом 3 равна сумме первого и последнего, т.е n и 3n умноженное на количество таких пар, а оно равно n/2
Складываем 2n+1 и n+2, эта сумма равна 3n+3
Значит a3+a6+a9+...a3n=(a[2n+1] + a[n+2])*n/2=23*n/2=736
n=736*2/23=64
А количество членов арифметической прогрессии равно 3*64=192
38) Функция 3+5x-x^2 достигает своего максимума в точке, которая является центром отрезка [x1,x2], где x1,x2 это корни квадратного уравнения 3+5x-x^2=0. По теореме Виета сумма корней приведенного квадратного уравнения равна коэффициенту перед первой степенью x со знаком минус. В нашем случае это 5, тогда функция принимает максимальное значение при x=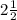 
. Найдем член последовательности при n=2 он равен 9,при n=3 он тоже равен 9.
Значит значение наибольшего члена последовательности равно 9.
ответ: 15-9=6.
1) x₁=0
x₂=-4
2)x=6
3)x=7
4)x=1/2+n, где n€Z
Пошаговое объяснение:
1)x=x/x+5
x*(x+5)=x
x²+5x-x=0
x²+4x=0
x(x+4)=0
x₁=0
x+4=0
x₂=-4
ответ: x₁=0; x₂=-4
2)√100+6x=8 ОДЗ: 100+6x>0
100+6x=8² 6x>-100
6x=64-100 x>-100/6
6x=36 x>-16 2/3
x=36:6
x=6 (удовлетворяет ОДЗ).
ответ: х=6
3) √7+6х=х ОДЗ: ║х≥0
х²-6х-7=0 ║7+6х≥0
D/4=9+7=16=4²>0
x₁=3+4=7 (удовлетворяет ОДЗ)
х₂=3-4=-1 (не удовлетворяет ОДЗ).
ответ: x=7
4) cos пи х=0
пи х=пи/2+пи n | :пи ,где n∈Z
х=1/2+n ,где n∈Z
ответ: x=1/2+n, где n∈Z.
(1290+8670)/30=332
900-712/8=811