Если проснуться рано утром и посмотреть в окно то можно посмотреть как падают снежинки с неба словно волшебная пыльца.Все деревья укутаны сияющем и чистым снежным одеялом все они погрузились в глубокий сон.Больше не слышно трели соловья, которая так нежно будила по утрам, а слышно только как трещат ветки от тяжести снега и кажется что вот-вот одна из хрупких веток сломается.Когда идешь по улице и поднимаешь взгряд на небо то видно как снежинки исполняют пируэты словно примы-балерины. И когда наблюдаешь за одной снежинкой понимаешь что она одна такая на всем белом свете...Все лишь одна, такая неповторимая и такая красивая...
Пошаговое объяснение:
Рисунок сразу с тремя графиками функций на рисунке в приложении.
В качестве исходного - график Y= cosX.
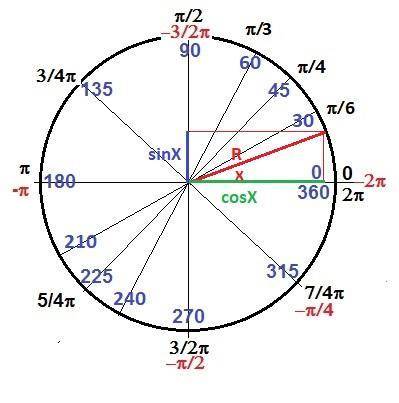
Эта функция от вращения точки по окружности радиусом = 1.
Rx/R = cosX, Ry/R = sinX. - на рисунке в приложении.
И так период функции Y = cosX = 2*π = 360°
Амплитуда значений таких функций не может быть больше R = 1.
Задание 1. Y = cos 2*x
Амплитуда остаётся такой же = 1, а вот период изменился и стал уже не 360°, а 360/2 = 180° = π.
На компьютерных графиках писать π - сложно. 30° = π/6. 60° = π/3.
СВОЙСТВА.
Амплитуда осталась равной единице, сдвига по оси Х - нет, а вот период стал в два раза меньше.
Задача 2 - Y= 1/2*cosX
Здесь совсем малое свойство - амплитуда уменьшается в два раза, па период так и остался - 2π = 360°
ДОПОЛНИТЕЛЬНО
Для построения тригонометрических функций надо запомнить значения функции в основных точках.
Х=0, У = 1
Х = π/3 = 60° У = √3/2 ≈ 0,87
Х = π/6 = 30° У = 0,5
Х = π/2 = 90° У = 0.

16*3=48 на три