ответ: 11
Пошаговое объяснение:
Пусть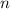 
- количество сторон
Возьмем первую вершину, соединим её с каждой другой вершиной, кроме данной и двух соседних, получается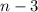 
диагоналей
Возьмем вторую вершину, соединим её с каждой другой вершиной, кроме данной и двух соседних, получается 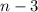диагоналей
Возьмем третью вершину, соединим её с каждой другой врешиной, кроме данной, двух соседних и первой, получается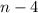 
диагоналей
Возьмем четвертую вершину, соединим её с каждой другой вершиной, кроме данной, двух соседних, первой и второй, получается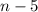 
диагоналей
И так далее
Веришину под номером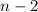 
нужно будет соединить только с вершиной под номером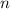
Две последние вершины итак уже соединены с другими
Итого диагоналей:
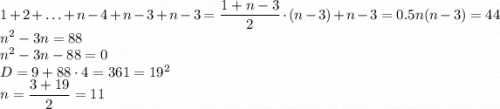
Пошаговое объяснение:
формула для вычисления объема тела вращения вокруг оси ОХ
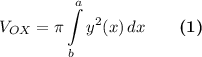
формула для вычисления объема тела вращения вокруг оси ОY
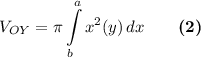
в нашем случае
![\displaystyle y=x^3\\x=\sqrt[3]{y}](/tpl/images/2008/5233/fadeb.png)
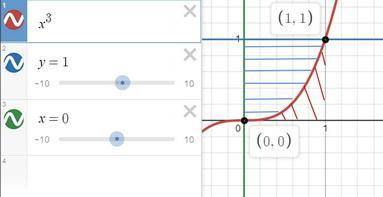
из графика видим, что пределы интегрирования в обоих случаях одинаковы
считаем
1. вокруг оси ОХ у нас область не прилегает к оси ОХ, поэтому будет объем Vох = V₁ - V₂, где
V₁ - объем цилиндра (R=1, h=1)который равен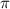 
(V= 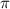R²h) и объем фигуры (вроде воронки), которую считаем по формуле (1), поэтому наш объем считаем
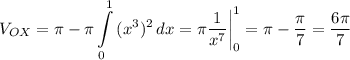
2. вокруг оси ОУ у нас дырки нет, область полностью прилегает к оси ОУ, поэтому просто считаем по формуле (2)
![\displaystyle V_{OY}=\pi \int\limits^1_0 {(\sqrt[3]{y} )^2} \, dy =\pi \int\limits^1_0 {y^{2/3}} \, dy =\pi \frac{3y^{5/3}}{5} \bigg |_0^1=\frac{3\pi}{5}](/tpl/images/2008/5233/69b3a.png)
на схеме
красная штриховка - "воронка"
синяя - наша фигура
2)16:8=2(кг) -на столько больше