Пошаговое объяснение:
1) 4х – 5 < 3x + 1
4х-3х<1+5
x<6
2) 3x + 7 > x + 15
3x-x>15-7
2x>8
x>4
3) 4 + 12х > 7 + 13х
4-7>13x-12x
-3>x
x<-3
4)7 – 4х < 6х – 23
7+23<6x+4x
30<10x
3<x
x>3
5) 4∙(x – 3) + 5x 3x=4х-12+15х=19х-12
Отсутствует знак неравенства. Нет возможности решить
6) 2∙(3x + 1) – x 3∙(x + 4)=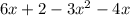
=2x+2-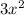
Отсутствует знак неравенства. Нет возможности решить
7) 7x + 4∙(x – 2) > 6∙(1 + 3x)
7x+4x-8>6+18x
11x-18x>6+8
-7x>14
x<-2
8)8 + 5х ≤ 3∙(7 + 2х)
8+5x≤21+6x
5x-6x≤21-8
-x≤13
x≥-13
Пошаговое объяснение:
591
Назовем угол при вершине "А", а углы при основании "В" и "С",тогда формула для нахождения углов "В" и "С": (180°-<А)/2. Решим примеры.
1) <В;С=(180°-100°)/2=40°
2) <В;С=(180°-84°)/2=48°
3) <В;С=(180°-36°)/2=72°
4) <В;С=(180°-24°)/2=78°
5) <В;С=(180°-126°)/2=27°
592
Для нахождения угла при вершине формула обратна: 180°-(<В*2). Решим примеры.
1) <А=180°-(35°*2)=110°
2) <А=180°-(42°*2)=96°
3) <А=180°-(57°*2)=66°
4) <А=180°-(72°*2)=36°
5) <А=180°-(88°*2)=4°
1/2 - это дробь
а и в - катеты, стороны треугольника, которые формируют прямой угол.
1/2 *а*в = 16
а*в = 16:1/2
а*в = 16*2
а*в = 32
чтобы вышло число 32 нужно умножить такие целые числа, как 1 и 32, 2 и 16, 4 и 8.
Таким образом: стороны треугольника могут быть 1см и 32см; 2см и 16см, 4см и 8см.
Проверяем:
32*1*1/2 = 32/2 = 16
2*16*1/2 = 32/2 = 16
4*8*1/2 = 32/2 = 16
ответ: 1см и 32см; 2см и 16см; 4см и 8см - могут быть стороны.