Дано уравнение параболы y=x^2-6x+6.
Вершина её хо =-в/2а = 6/(2*1) = 3, уо = 9-18+6 = -3.
Угловой коэффициент прямой, проходящей через начало координат и вершину параболы, равен к1 = -3/3 = -1.
Производная этой функции равна y' = 2x - 6.
Уравнение нормали к параболе имеет вид у(н) = уо - (1/y'(xo))*(x - xo).
Величина "- (1/y'(xo))" это угловой коэффициент к2 нормали, он равен: к2 = -1/к1 = -1/(-1) = 1.
Приравняем (- (1/y'(xo))) = 1 и подставим y' = 2xо - 6.
(-1/(2xо - 6)) = 1. Отсюда 2xо - 6 = -1, 2хо = 5, хо = 5/2 = 2,5 это точка А пересечения нормали и параболы. уо = (25/4)- (30/2) + 6 = -11/4 = -2,75.
Подставив координаты точки А в уравнение нормали, получаем:
у(н) = х - (21/4).
ответ: Первая труба наполнит бассейн за 19.34 часа, вторая за 24.45 часа и третья за 5.84 часа
Пошаговое объяснение:
Введем понятие производительности трубы - какую часть от всего бассейна она наполнит за 1 час. Тогда у первой трубы производительность p1, у второй p2 и у третьей p3.
Получим три уравнения вытекающие из условий задачи:
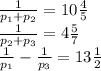
В первых двух решим пропорцию, а в третьем приведем к общему знаменателю:
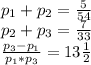
Из второго уравнения вычтем первое, а в третьем выразим произведение производительностей первой и третьей трубы:
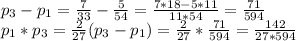
В первом выразим производительность третьей через первую и подставим во второе уравнение:
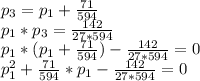
Решим последнее квадратное уравнение:
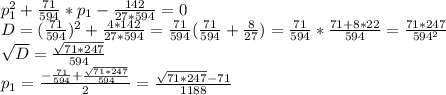
При решении взяли дискриминант положительный, т.к. производительность не может быть отрицательной. Дальнейшее решение возможно только в приближенных числах:
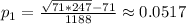
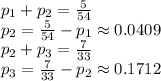
По найденным производительностям найдем сколько времени понадобится каждой трубе для заполнения бассейна:
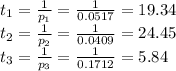
Моя Родина начинается с маленькой речки на даче, с куста смородины, листочки которой так вкусно пахнут. Родина – это поле с огромным небом над ним, где мы пускали воздушного змея и любовались радугой. И лес, где так сильно пахнет земляникой и хвоей. Разлитый, как молоко, туман, в котором можно спрятаться…
Наверное, с этого начинается для меня Родина.