Задачу можно интерпретировать как 250 опытов с фиксированной вероятностью успеха и неудачи в каждом отдельном испытании, т.е. по факту мы имеем биномиальное распределение, применима формула Бернулли
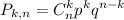
или в нашем случае
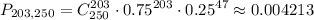
Если мощного калькулятора под рукой нет, то лучше вместо биномиального использовать нормальное распределение. Это допустимо, ведь из центральной предельной теоремы следует что при неограниченном возрастании числа опытов ф-я распределения будет неограниченно приближаться к нормальному распределению (с мат. ожиданием 0 и дисперсией 1)
1)
t = 3 ч
d = 2 ч
m = 6 ч
1 : 3 = 1/3 (бас/час) - производительность первой трубы.
1 : 2 = 1/2 (бас/час) - производительность второй трубы.
1 : 6 = 1/6 (бас/час) - производительность третьей трубы.
1/3 + 1/2 + 1/6 = 6/6 = 1(бас/час) - общая производительность трех труб.
Значит, бассейн наполнится за 1 час, если будут открыты все трубы.
ответ: 1 час.
2)
t = 4 ч
d = 5 ч
m = 20 ч
1 : 4 = 1/4 (бас/час) - производительность первой трубы.
1 : 5 = 1/5 (бас/час) - производительность второй трубы.
1 : 20 = 1/20 (бас/час) - производительность третьей трубы.
1/4 + 1/5 + 1/20 = 1/2 (бас/час) - общая производительность трех труб.
1 : 1/2 = 2 (ч) - за такое время наполнится бассейн, если будут открыты все трубы.
ответ: 2 часа.
3)
t = 3 ч
d = 4 ч
m = 12 ч
1 : 3 = 1/3 (бас/час) - производительность первой трубы.
1 : 4 = 1/4 (бас/час) - производительность второй трубы.
1 : 12 = 1/12 (бас/час) - производительность третьей трубы.
1/3 + 1/4 + 1/12 = 2/3 (бас/час) - общая производительность трех труб.
1 : 2/3 = 1,5 (ч) - за такое время наполнится бассейн, если будут открыты все трубы.
ответ: 1,5 часа.