Пошаговое объяснение:
это степенной ряд. запишем его в общем виде
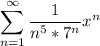
областью сходимости степенного ряда является интервал (-R;R), где R - радиус сходимости и равен
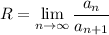
посчитаем этот предел
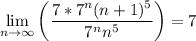
таким образом, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-7;7)
теперь посмотрим сходимость ряда на концах этого интервала.
пусть х = -7, тогда мы получим ряд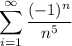 
, это числовой знакочередующийся ряд
надо исследовать его на сходимость. исследуем по признаку Лейбница
а) по первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего
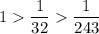- выполняется
б) по второму признаку Лейбница предел ряда по модулю должен стремится к 0
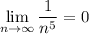выполняется
т.е. ряд сходится x = -7 - точка сходимости
теперь пусть х = 7
тогда всё просто, как в первом случае, только ряд не знакочередующийся. он сходится x = 7 - точка сходимости
и вот получаем,
данный степенной ряд является сходящимся на интервале [-7;7]
12+12√3 cм
Пошаговое объяснение:
Для того, чтобы найти периметр нам нужно знать длины двух сторон: P=(AB+CD)*2. Как мы знаем, угол при вершине С в треугольнике ACD равен половине угла AOD, а если не знаем, то докажем: пусть угол в 120 градусов равен фи, тогда
∠DOC=180º-∠AOD=180º-φ (как смежные).
Треугольник COD — равнобедренный с основанием CD
(OC=OD по свойству диагоналей прямоугольника). Тогда
![\[\angle OCD = \frac{{{{180}^o} - \angle AOD}}{2} = \frac{{{{180}^o} - ({{180}^o} - \varphi )}}{2} = \] \[ = \frac{{{{180}^o} - {{180}^o} + \varphi }}{2} = \frac{\varphi }{2}.\]](/tpl/images/1774/5491/41e37.png)
(как угол при основании равнобедренного треугольника).
Следовательно мы доказали то, что хотели
, значит он(угол С) равен 60 градусов, тогда угол A в этом же треугольнике ACD равен 30 градусов(т.к. треугольник прямоугольный), тогда по следствию из Т. Пифагора, катет лежащий напротив угла в 30 градусов(СD) равен половине гипотенузы(AC=2AO), следовательно АО=СД, а значит этот треугольник ОСD равносторонний, что можно было понять чуть раньше, т.к. угол при вершине О = 60 градусов и угол при вершине С тоже 60, но о том, что если у треугольника углы по 60 градусов, то он равносторонний знают не все, поэтому довел до этапа с длинами. Найдем длину АD как катет по Т. Пифагора. АС=12, СД=6, следовательно АД равно
AD=√144-36=6√3
А теперь найдем периметр: 2*(6√3+6)=12+12√3 cм
по течению: к собственной прибавить скорость течения
против течения: от собственной отнять скорость тесения