НОД
1) Раскладываем на простые множители
2) перемножаем общие множители
НОК
1) Раскладываем на простые множители
2) Подчеркиваем в меньшем числе множители,которых нет в большем
3) Недостающие множители добавляем к множителям большего числа и перемножаем их:
4 и 10
НОД
4=2*2
10=2*5
Общий множитель: 2
НОД (4; 10)=2
НОК
10=2*5
4=2*2
НОК (4; 10)=2*5*2=20
15 и 18
НОД
15=3*5
18=2*3*3
Общий множитель: 3
НОД (15;18)=3
НОК
15=3*5
18=2*3*3
НОК (15;18)=2*3*3*5=90
6 и 14
НОД
14=2*7
6=2*3
Общий множитель: 3
НОД (6; 14) = 2
НОК
14=2*7
6=2*3
НОК (6;14)=2*7*3=42
20 и 24
НОД
24=2*2*2*3
20=2*2*5
Общие множители : 2; 2
НОД (20; 24)=2*2=4
НОК
24=2*2*2*3
20=2*2*5
НОК (20; 24)=2*2*2*3*5=120
8 и 12
НОД
12=2*2*3
8=2*2*2
Общие множители: 2; 2
НОД(12;8)=2*2=4
НОК
12=2*2*3
8=2*2*2
НОК(12;8)=2*2*3*2=24
26 и 39
НОК
39=3*13
26=2*13
Общий множитель: 13
НОД(26;39)=13
НОК
39=3*13
26=2*13
НОК(26;39)=3*13*2=78
Пошаговое объяснение:
Дано:
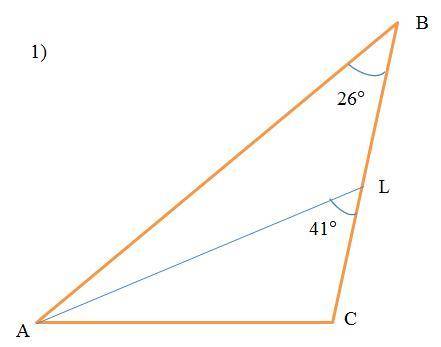
В ΔABC
∠ABC=∠ABL=26°
Уточнение: в условии 1) ∠ALC=41°, а на рисунке 2) ∠LAC=41°. Поэтому задачу решаем для обоих случаев.
Найти: ∠ACB
1) Так как ∠ALC=41°, то смежный с ним ∠ALB=180°-41°=139°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠АLB+∠АBL+∠BАL=180°
Отсюда:
∠BAL = 180° - ∠ALB - ∠АBL = 180° - 139° - 26° = 15°.
Биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠BAL = 2·15° = 30°.
Ещё раз используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 30° - 26° = 124°.
ответ: ∠ACB = 124°.
2) Так как ∠LAC=41° и биссектриса делит ∠BАC пополам, то
∠BАC = 2·∠LАC = 2·41° = 82°.
Используем свойство: сумма внутренних углов треугольника равна 180°:
∠BАC+∠АBC+∠АCB=180°
Отсюда:
∠ACB = 180° - ∠BАC - ∠АBC = 180° - 82° - 26° = 72°.
ответ: ∠ACB = 72°.
Значит это 6 гектаров.