№1
Дано:
∆АВС – равносторонний,
SC=12,
AB=4,
Углы SCA и SCB – прямые.
Найти: SA, SB
Так как ∆ABC – равносторонний по условию, то АС=ВС=АВ=4.
Углы SCA и SCB – прямые по условию, тогда ∆SCA u ∆SCB – прямоугольные.
По теореме Пифагора в ∆SCA:
SA²=SC²+AC²
SA²=12²+4²
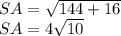
По теореме Пифагора в ∆SCB:
SB²=SC²+BC²
SB²=12²+4²
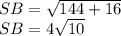
ответ: 4√10.
№2
Дано:
∆АВС – равнобедренный с основанием CD (не равносторонний так как CE≠CD),
CE=ED=10 см,
CD=16 см,
SE=2 см,
Угол SEO=90°,
ЕО – высота ∆АВС.
Найти: SO
Высота равнобедренного треугольника, проведенная к основанию, так же является медианой.
Следовательно ЕО – медиана, значит CO=DO=0,5CD=16*0,5=8 см.
Так как ЕО – высота, то угол ЕОС=90°, тогда ∆ЕОС – прямоугольный.
В ∆ЕОС по теореме Пифагора:
ЕС²=СО²+ЕО²
10²=8²+ЕО²
ЕО²=100–64
ЕО=√36
ЕО=6 см
Так как угол SEO=90° по условию, то ∆SEO – прямоугольный.
В ∆SEO по теореме Пифагора:
SO²=SE²+EO²
SO²=2²+6²
SO²=4+36
SO=√40
SO=2√10 см.
ответ: 2√10 см.
Пусть х - площадь первой комнаты, тогда 1,4х - площадь второй комнаты
Составим уравнение:
х + 1,4х = 40,8
2,4х = 40,8
х = 40,8 : 2,4
х = 17 - площадь первой комнаты
1,4 * 17 = 23,8 - площадь второй комнаты
2.
(9,52 : 34) * 4,5 - 0,5 = 0,76
1) 9,52 : 34 = 0,28
2) 0,28 * 4,5 = 1,26
3) 1,26 - 0,5 = 0,76
3.
(5,4у + 8,3) * 2,1 = 23,1
5,4у + 8,3 = 23,1 : 2,1
5,4у + 8,3 = 11
5,4у = 11 - 8,3
5,4у = 2,7
у = 2,7 : 5,4
у = 0,5
ответ: 0,5