AC=10 см
Пошаговое объяснение:
Розв'язання:
Нехай дано ∆АВС, МК - серединний перпендикуляр до сторони АВ,
т. М належить сторон!і ВС, ВС = 16 см, Р∆АМС = 26 см. Знайдемо сторону АС.
Розглянемо ∆АМК i ∆BMK.
1) АК = KB (т. К - середина АВ);
2) ∟AКM = ∟BKM = 90° (МК ┴ АВ);
3) MК - спільна.
Отже, ∆АМК = ∆BMК за I ознакою, з цього випливає, що AM = MB.
Р∆АМС = АС + АМ + СМ (т.я. АМ = МВ, то Р∆АМС = АС + МВ + СМ).
26 = АС + MB + CM, MB + СМ = СВ = 16 см.
26 = АС + 16; АС = 26 - 16; АС = 10 см.
Biдповідь: AC = 10 см.
1. V(параллелепипеда)=4*8*16=512 см³
ребро куба а=∛512=8 см.
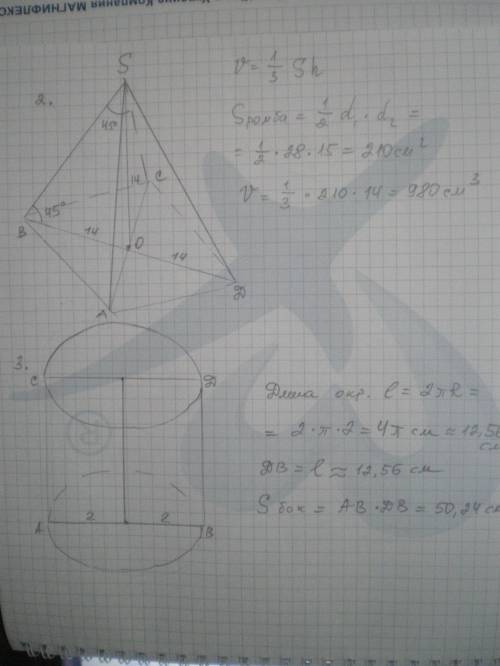
2. Пусть дана пирамида SABCD, SО - высота, АС=15 см, ВD=28 см, ∠SBO=45°. Найти объём пирамиды V.
В основании пирамиды лежит ромб, диагонали ромба в точке пересечения делятся пополам. Значит, ВО=ОД=28:2=14 см.
Рассмотрим Δ SВО - прямоугольный. ∠SBO=45°, значит и ∠ВSB=45°, т.е. ΔSВО - равнобедренный и SВ=SО=14 см.
Найдем площадь основания по формуле
S(ромба)=1\2 * АС * ВD = 1\2 * 28*15 = 210 см²
Найдем объем пирамиды
V=1\3 * S * h = 1\3 * 210 * 14 = 980 cм³.
3. Пусть дан цилиндр, АВ - диаметр, АВ=4 см, ДВ - высота, ДВ=L. Найти S боковой поверхности.
L=2πR=2*3,14*2≈12,56 см.
S боковой поверхности=АВ*ВД=4*12,56=50,24 см²
8см
Пошаговое объяснение:
1)4+4+4+4=16(см)-периметр прямокутника 2)16:2=8(см)-довжина відрізка