134°
Пошаговое объяснение:
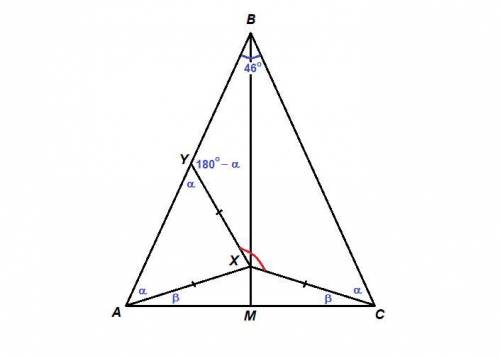
XY = XA, значит ΔAXY равнобедренный с основанием AY, углы при основании равны:
∠XAY = ∠XYA = α
В равнобедренном треугольнике медиана, проведенная к основанию, является высотой, т.е. ВМ - серединный перпендикуляр к АС.
Любая точка серединного перпендикуляра к отрезку равноудалена от его концов.Тогда XA = XC, ΔХАС равнобедренный с основанием АС, углы при основании равны:
∠ХАС = ∠ХСА = β.
ΔАВС равнобедренный, значит углы при основании равны.
∠ВАС = ∠ВСА
α + β = ∠ВАС
∠ВСХ = ∠ВСА - β = ∠ВАС - β = α
∠BYX = 180° - ∠XYA = 180° - α, так как эти углы смежные.
Сумма углов выпуклого четырехугольника равна 360°.В четырехугольнике YBCX:
180° - α + 46° + α + ∠YXC = 360°
226° + ∠YXC = 360°
∠YXC = 360° - 226° = 134°
0,5х=х
0,5х-х=0
-0,5х=0
х=0
2)3,4у-1=1,2у
3,4у-1,2у=1
2,2у=1
у=1\2,2
3)0,7х=0,5х+3
0,7х-0,5х=3
0,2х=3
х=3\0,2
х=15