ДА
Пошаговое объяснение:
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Для того, чтобы найти синус по известному косинусу, 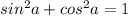
Тангенс по известному косинусу 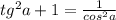
Котангенс по известному синусу или наоборот 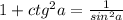
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: 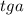 ×
× 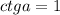
10 С = 3 Я + 1 Г
2 С + 1 Я = 1 Г
1 Г = ? С
Решение.
1-й с п о с о б. Заменяем яблоки грушами.
1 Г - 1 Я = 2 С настолько одна груша тяжелее одного яблока
2 * 3 = 6 (С) столько слив надо добавить, если 3 яблока заменить 3-мя грушами.
10 С + 6 С = (3 + 1) Г равенство с заменой яблок грушами.
16 С = 4 Г
4 С = 1 Г
ответ: 1 груша по массе равна 4 сливам.
2-й с п о с о б. Заменяем грушу яблоком.
1 Г = 1 Я + 2 С по условию.
10 С = 3 Я + (1 Я + 2 С) так как груша тяжелее яблока на две сливы
10 С = 4 Я + 2С равенство без груш
8 С = 4 Я убрали лишние сливы из обеих частей равенства.
2 С = 1 Я стольким сливам равно одно яблоко
1 Г = (2С)+ 2 С поскольку груша на две сливы тяжелее яблока
1 Г = 4 С --- стольким сливам равна одна груша.
ответ: 4 сливам равна 1 груша по массе.
2х кусты сирени
х + 2х = 540
3х = 540
х = 540 / 3
х = 180
180 * 2 = 360
ответ:Посадили 180 кустов шиповника и 360 кустов сирени