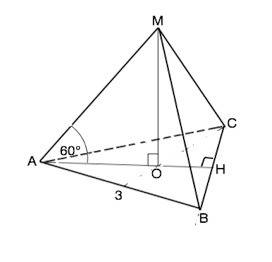
Объём пирамиды равен 1/3 произведения площади снования на высоту. V=S•h/3 Пирамида правильная, следовательно, её основание – правильный треугольник, вершина проецируется в центр описанной около основания окружности (точку пересечения высот, медиан, биссектрис), и все ребра равны между собой. Обозначим пирамиду МАВС. её высоту МО, высоту основания АН. Отрезок АО - радиус описанной окружности и равен 2/3 высоты АН. Все углы правильного треугольника равны 60°⇒ АН=АВ•sin60°=3√3)/2 ⇒ AO=АН•2/3=3/√3=√3. Из прямоугольного ∆ АМО высота МО=AO•tg60°=√3•√3=3 см Для правильного треугольника S=a²√3/4 S(ABC)=9√3/4 см² Объём (МАВС)= 9√3:4)•3:3=9√3:4 см³
В основании пирамиды лежит параллелограмм. Его высоты можно найти через стороны и площадь. Высота к стороне 36 см равна 360/36=10 см, а высота к стороне 20 см равна 360/20=18 см.
Находим далее высоты каждой боковой грани - треугольника. По теореме Пифагора для треугольника со сторонам 12 и 5 см третья сторона равна 13 см., а для треугольника со сторонами 12 и 9 см третья сторона равна 15 см.
Поскольку пирамида не является правильной, ее боковая поверхность определяется через сумму площадей боковых граней. Т.е. это сумма площадей четырех треугольников. причем противоположные боковые грани равны.
S бок = 2(15*10+12*18)=366 см2.