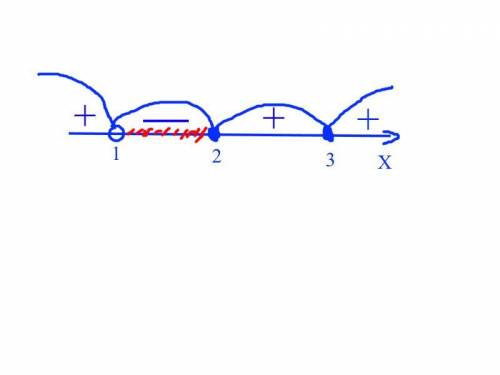
1) y = |x-5| - |3-x| + |x+4| + |x+2|
График будет состоять из нескольких прямых.
При х < - 4 будет
y = 5-x-(3-x)+(-x-4)+(-x-2) = 5-x-3+x-x-4-x-2 = -2x-4
При x € [-4; -2) будет
y = 5-x-(3-x)+(x+4)+(-x-2) = 5-x-3+x+x+4-x-2 = 4
При x € [-2; 3) будет
y = 5-x-(3-x)+x+4+x+2 = 5-x-3+x+x+4+x+2 = 2x+8
При x € [3; 5) будет
y = 5-x-(x-3)+x+4+x+2 = 5-x-x+3+x+4+x+2 = 14
При x >= 5 будет
y = x-5-(x-3)+x+4+x+2 = x-5-x+3+x+4+x+2 = 2x+4
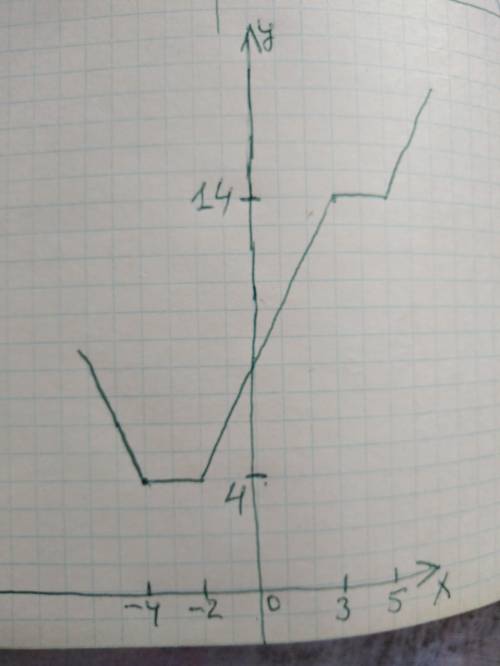
График на первом рисунке.
2) y = |x| + x
График состоит из двух лучей.
При x < 0 будет y = - x + x = 0
При x >= 0 будет y = x + x = 2x
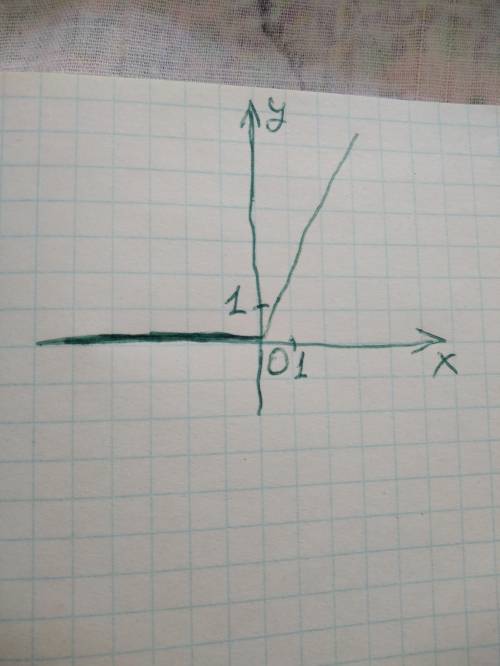
График на втором рисунке.
x ∈ (1; 2] ∪ {3}
Пошаговое объяснение:
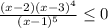
решим неравенство методом интервалов. Для этого приравняем и числитель и знаменатель к нулю:
x-2=0; x=2
x-3=0; x=3
x-1=0; x=1
изобразим точки на координатной прямой. Точка "1" будет выколота, так как она обнулит знаменатель, а на 0 делить нельзя. Точки "2" и "3" будут закрашенными, т.к знак неравенства "меньше или равно" (см рис)
знак крайнего правого интервала будет + (можно взять число "100" и подставить в неравенство), дальше "+"; "-"; "+" (подставляем точки из этих интервалов в неравенство и ищем знак)
т.к знак неравенства "≤0", то выбираем интервалы с "-"
также отдельно берем точку "3", т.к она обнулит числитель, а это нас устраивает
x ∈ (1; 2] ∪ {3}