Пусть х(ч)-потребуется первой машинистке, чтобы перепечатать рукопись. Всю работу примем равной 1. Тогда за 1 час первая машинистка перепечатает 1/х рукописи, а вторая машинистка за час перепечатает 1/(х-7) рукописи, вместе затратив на всю работу за 1 час 1/12ч. Составим и решим уравнение:
1/х+1/(х-7)=1/12, ОДЗ: х не равен 0 и 7.
Умножим обе части уравнения на 12х(х-7), получим уравнение:
12(х-7)+12х=х(х-7),
12х-84+12х-х(в квадр)+7х=0,
-х(в квадр)+31х-84=0,
Д=961-336=625, 2 корня
х=(-31+25)/-2=3-не является решением задачи
х=(-31-25)/-2=28
28(ч)-потребуется 1 машинистке
28-7=21(ч)-потребуется второй машинистке чтобы перепечатоть рукопись
По вашим данным составим уравнение, позначив часть книги которую прочитал Денис во второй ден как х, соответственно в 1 день он прочитал х+1/9.
Соответственно за первый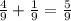
Проверяем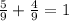
- все верно)