Пошаговое объяснение:
Дана функция y = 3 * sin(x + П/6) - 2.
Область определения - все допустимые значения переменной x.
Значение переменной X здесь определяется областью определения функции y = sinx - вся числовая ось. Так как здесь к аргументу добавлено число П/6, то значения аргумента не меняются.
Значением синуса определенного угла (x +П/6) может быть число от -1 до 1. Напишем это:
-1 < sin(x + П/6) < 1;
Умножим все части неравенства на 3:
-3 < 3 * sin(x + П/6) < 3;
Ко всем частям неравенства прибавим -2:
-5 < 3 * sin(x + П/6) + 2 < 1.
Область значения функции - все числа от -5 до 1.
Рассмотрим первое слагаемое (82n). Произведение четного числа на любое другое целое дает нам четное число (правило 2).
Второе слагаемое должно быть нечетным, так как произведение двух нечетных чисел нечетно (правило 1).
И сумма четного и нечетного чисел обязательно нечетна (3), искомое число будет нечетным, что и требовалось доказать!
Примечание:
Необходимые правила:
(1) Если нечетное число умножить на нечетное, то получится тоже нечетное (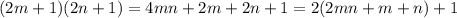
).(2) Произведение четного числа на любое натуральное (или целое) всегда будет четным (если умножаем на нечетное:
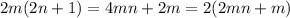; если на четное: 
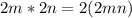).(3) Если сложить четное и нечетное числа, то получится нечетное число (
).
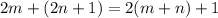48:х<8
если вместо буквы х подставить число 6, неравенство 48:х<8 обратится в верное числовое неравенство:
48:8<8
6<8
Но это не единственное значение х, при котром неравенство обращается в верное числовое неравенство.
Если х=12 ,то 48:12<8 - верное неравенство;
х=16 , то 48:16<8 - верное неравенство;
х=24 , то 48:24<8 - верное неравенство;
х=48 , то 48:48<8 - верное неравенство;
х=0 , то 48:0<8 - верное неравенство.
Значит решением неравенства 48:х<8 являются числа 48, 24, 16, 12, 8, 0.