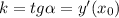
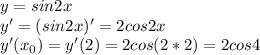
Надо решить такое уравнение:
2x^3 + 9x^2-4=0
Для вычисления корней этого кубического уравнения используем тригонометрическую формулу Виета, которая работает для уравнений вида:
x^3 + ax^2 + bx + c = 0. Если уравнение не такого вида, то его можно получить поделив всё уравнение на коэффициент возле x^3.
В нашем случае a = 4.5, b = 0 и c = −2.
1. Вычисляем
Q=(a2- 3b)/9 2,25
R=(2a3 - 9ab + 27c)/54 2,375
2. Вычисляем
S = Q^3 - R^2 5,75
3. a) Если S>0, то вычисляем
φ=(arccos(R/Q3/2))/3 0,703703704
И наше уравнение имеет 3 корня (вещественных):
x1= - 2(Q)1/2cos(φ) - a/3 = -4,396531134.
x2= - 2(Q)1/2cos(φ+2π/3) - a/3 = 0,624712566.
x3= - 2(Q)1/2cos(φ-2π/3) - a/3 = -0,728181432.
См. Пошаговое объяснение.
Пошаговое объяснение:
д) -4,3 · 5,1 = -21,93
Правило: при умножении отрицательного числа (-4,3) на положительное число (+5,1; знак + не ставится) произведение должно быть со знаком минус.
Для всех случаев умножения и деления говорят кратко: "минус на плюс даёт минус". Например: 4,3 · (-5,1) = -21,93 Ещё пример: (-8) : 4 = -2. Ещё пример: 8 : (-4) = - 2.
е) -2,7 · (-6,4) = 17,28
Правило: при умножении отрицательного числа (-2,7) на отрицательное число (-6,4) произведение должно быть со знаком плюс.
Для всех случаев умножения и деления говорят кратко: "минус на плюс - даёт плюс".
ж) -1 · (-3,84) = 3,84
Правило: при умножении отрицательного числа (-1) на отрицательное число (-3,84) произведение должно быть со знаком плюс.
Для всех случаев умножения и деления говорят кратко: "минус на плюс - даёт плюс".
з) - 7,2 · 0 = 0
Правило: при умножении любого числа на ноль получается ноль. Знак перед нулём не ставится.