Если нужно, могу решить любое задание. Как их делать я вроде расписал. Как рисовать рисунок тоже, так что если на моем ничего не понятно, думаю ты сам(а (на) нарисовать такой рисунок. За качество рисунка не ругайте, пэйнтом владею плохо и вообще у автора лапки :)
Пошаговое объяснение:
Покажу на примере 5.38 (1)
17х - 2 > x - 4
3 - 9x < 1 - x
16x > 2
-8x < -2
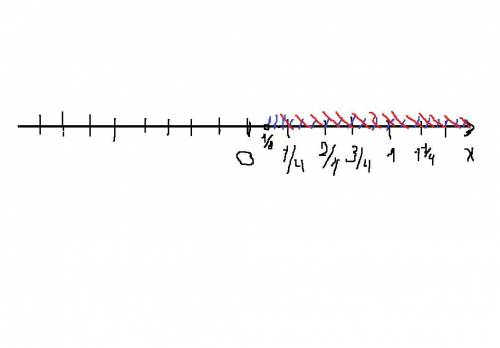
x > 1/8
x > 1/4
Дальше идет рисунок: числовая прямая, на которой мы отмечаем точки, которые ограничивают х (в нашем случае 1/8 и 1/4). Показываем область определения обоих значений (у меня это полосы разных цветов, которые на некотором участке пересекаются. Тот (те) участки, на которых они пересекаются и есть область определения х. А ОО - это и есть ответ. У тебя в номере 5.38 нужно изобразить его на числовой прямой (числовая ось это то же самое). Это мы сделали. Чтобы записать ответ как в номере 5.39 нужно взять крайние точки ОО (в нашем случае 1\4 и +∞) и записать их через точку с запятой от большего к меньшему, а потом поставить скобки, исходя из строгости знака в предварительном ответе (если знак < или >, то скобки круглые (), а если знак ≤ или ≥, то скобки квадратные []) У нас знак >, значит скобки круглые.
ответ: (1\4;+∞)
Проще всего решение по формулам Крамера.
Записываем его в виде "наклонных полосок".
Первый определитель:
1 -5 -2| 1 -5
-5 4 3| -5 4
5 -3 2| 5 -3 =
= 1 *4* 2 + -5* 3* 5 + -2* -5* -3 -
-5* -5* 2 - 1* 3* -3 - -2* 4* 5 =
= 8 + -75 + -30 - 50 - -9 - -40 = -98.
Остальные определители находятся аналогично.
1 -5 -2 -22 Определитель
-5 4 3 12 -98
5 -3 2 2
Заменяем 1-й столбец на вектор результатов B:
-22 -5 -2
12 4 3 Определитель
2 -3 2 -196
Заменяем 2-й столбец на вектор результатов B:
1 -22 -2
-5 12 3 Определитель
5 2 2 -392
Заменяем 3-й столбец на вектор результатов B:
1 -5 -22
-5 4 12 Определитель
5 -3 2 -196
x = -196 /-98 = 2
y= -392/ -98 = 4
z= -196/-98 = 2.
Объем шара V = 4/3 * пи *R^3
Радиус шара равен половине диаметра : 30 / 2 = 15 см
S = 4 * 3.14 *15^2 = 2826 см2
V = 4/3 *3.14 *15^3 = 14130 см3