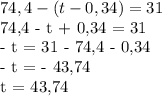
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент: b = 1 + 0,01a.
После первой выплаты сумма долга составит:
S1 = Sb − X.
После второй выплаты сумма долга составит:
S2 = S1b − X = (Sb − X)b − X = Sb² − (1 + b)X.
После третьей выплаты сумма оставшегося долга равна:
S3 = Sb³ - (1-b+b²)X = Sb³ -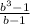
· X
После четвертой выплаты сумма оставшегося долга равна:
S4 =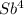 
- (1 + b +b² + b³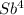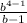)X = 
- 
· X
По условию четырьмя выплатами Алексей должен погасить кредит полностью, поэтому 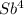- 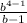· X = 0.
Потом выражаешь из этого выражения X и при S = 6902000 и а = 12,5, получаем: b = 1,125 получается:
X = 
рублей
ответ: 3 и 9
Пошаговое объяснение: Так как разность двух чисел равна 6, то уменьшаемое (1 число) больше вычитаемого (2 число) на 6. Значит 1 число можно представить как сумму 2 числа и 6.
Тогда, если сложить эти два числа, то мы получим сумму удвоенного 2 числа и 6, что равно 12. Откуда 2 число в два раза меньше разности 12 и 6, то есть оно равно 3. Чтобы при сложении двух чисел (1 числа и 3) получилось 12, второе слагаемое (1 число) должно быть равно 9.
Алгебраическая запись:
Пусть a -- второе число, тогда a+6 -- первое число. Составим уравнение, используя условие суммы:
a + (a + 6) = 12
2a + 6 = 12
2a = 6
a = 3 -- второе число
a + 6 = 3 + 6 = 9 -- первое число
