Для решения данной задачи мы будем использовать пропорции.
1. Пусть x - сумма денег, которую получит спортсмен, занявший 1-е место.
2. Тогда суммы денег, которые получат спортсмены, занявшие 2-е и 3-е места, будут соответственно 3x и x/5.
Теперь мы можем составить пропорцию:
1:3:5 = x:3x:x/5
Для решения этой пропорции, мы можем умножить крест на крест:
1 * x/5 = 3 * x
Получим:
x/5 = 3x
После этого мы можем перенести все переменные на одну сторону уравнения:
x - 3x/5 = 0
Далее выносим x за скобки и переносим его на другую сторону уравнения:
5x - 3x = 0
Теперь складываем коэффициенты при x:
2x = 0
Делим обе части уравнения на 2:
x = 0 / 2
Получим:
x = 0
Исходя из этого, получаем, что сумма, которую получит спортсмен, занявший 1-е место, составляет 0 р.
Теперь мы можем найти суммы денег, которые получат спортсмены, занявшие 2-е и 3-е места.
Спортсмен, занявший 2-е место, получит: 3x = 3 * 0 = 0 р.
Спортсмен, занявший 3-е место, получит: x/5 = 0/5 = 0 р.
Таким образом, каждый спортсмен, занявший призовое место, получит 0 р.
Пошаговое объяснение:
1) 4х – 5 < 3x + 1
4х-3х<1+5
x<6
2) 3x + 7 > x + 15
3x-x>15-7
2x>8
x>4
3) 4 + 12х > 7 + 13х
4-7>13x-12x
-3>x
x<-3
4)7 – 4х < 6х – 23
7+23<6x+4x
30<10x
3<x
x>3
5) 4∙(x – 3) + 5x 3x=4х-12+15х=19х-12
Отсутствует знак неравенства. Нет возможности решить
6) 2∙(3x + 1) – x 3∙(x + 4)=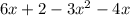
=2x+2-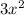
Отсутствует знак неравенства. Нет возможности решить
7) 7x + 4∙(x – 2) > 6∙(1 + 3x)
7x+4x-8>6+18x
11x-18x>6+8
-7x>14
x<-2
8)8 + 5х ≤ 3∙(7 + 2х)
8+5x≤21+6x
5x-6x≤21-8
-x≤13
x≥-13